Bonjour
tu veux parler de géométrie descriptive ?

Oui,en géométrie descriptive.

Bonjour et bonne année david1972,

Une question se pose: comment est définie ta surface composée?

  De ce que je vois, je déduis qu'il y a deux demi cylindres (de sections normales à leurs axes elliptiques) raccordés par deux surfaces planes parallèles en forme de triangles.

  Tu confirmes ?

  Si c'est le cas l'épure consiste à construire l'intersection du grand cylindre par des droites (toutes parallèles: les génératrices des deux demi cylindres) à l'aide de plans auxiliaires bien choisis et par deux plans parallèles (les deux triangles).

  

Bonjour Lake et tous mes vœux.Donc,les bases de la surface composée  sont circulaires (l'une circulaire,l'autre en forme d'oblond) et cette surface composée intersecte un demi-cylindre à base circulaire dont sa section normale est elliptique je pense.Je t'ai fait des vues en trois dimensions des pièces.
Nota :Les parois hautes de la pièce cylindrique sont bien plane ainsi que les triangles de la surface composée.

Bien cordialement,

Re Bonjour Lake,pourrais tu s'il te plaît me faire l'epure  qui permet de défini la courbe d'intersection ?

Les choses ne se sont pas bien passées

J'avais choisi comme plan auxiliaire un plan parallèle aux deux faces de la surface composée et qui contenait 2 génératrices des demi cylindres (une par demi cylindre).
Ce plan coupe le grand cylindre suivant une ellipse. Une intersection génératrice/ellipse fournit un point de l'intersection cylindre de la surface composée/cylindre principal.

Après avoir geobrisé pendant ... un certain temps, je suis passé au plus plaisant: activer la fonction lieu de Geogebra pour voir apparaître les projections de l'intersection cherchée.

Hélas, 3 fois hélas, la fonction lieu ne marche pas et je me sens tout bête _{(et fâché)}. Je crois que cette fonction digère mal les intersections droites/coniques.
Bien sûr, avec le mode "trace", on voit quelque chose mais c'est très moche et je préfère ne rien publier pour l'instant.

Il faut donc que je reprenne l'affaire quasiment à zéro mais je n'ai plus le temps maintenant. Donc probablement demain...

D'accord,

Concernant ton logiciel,est-ce un logiciel  de D.A.O?Quel est sont prix et le coût de la formation ?

La partie supérieure du grand cylindre n'intervenant pas dans l'intersection, j'ai réalisé l'épure avec un cylindre complet pour me faciliter la vie.

J'ai choisi d'utiliser un  plan auxiliaire frontal (parallèle au plan frontal de projection).

Ce plan recoupe le demi cylindre gauche du solide composé suivant une génératrice (en bleu) (qu'on voit aussi en vue de gauche en ).

Ce même plan recoupe le cylindre principal suivant une ellipse reportée en vraie grandeur en bleu sur la projection frontale.

Sur cette projection frontale l'intersection de et de cette ellipse donne un  la projection frontale d'un point courant de l'intersection en

Une ligne de rappel permet d'obtenir sa projection horizontale en . (On voit aussi ce point en vue de gauche en )

Lorsque le point décrit la demi circonférence en projection horizontale, le point d'écrit l'arc en PH, l'arc en PF et l'arc en V de G.

Par symétrie on obtient les autres arcs en PH et PF.

Reste l'intersection du cylindre principal par les deux plans (frontaux eux aussi) du solide composé. Ce sont des arcs d'ellipses. Ils sont reportés en vraie grandeur en PF: et . Ils correspondent en PH aux segments et et aux segments et en V de G.



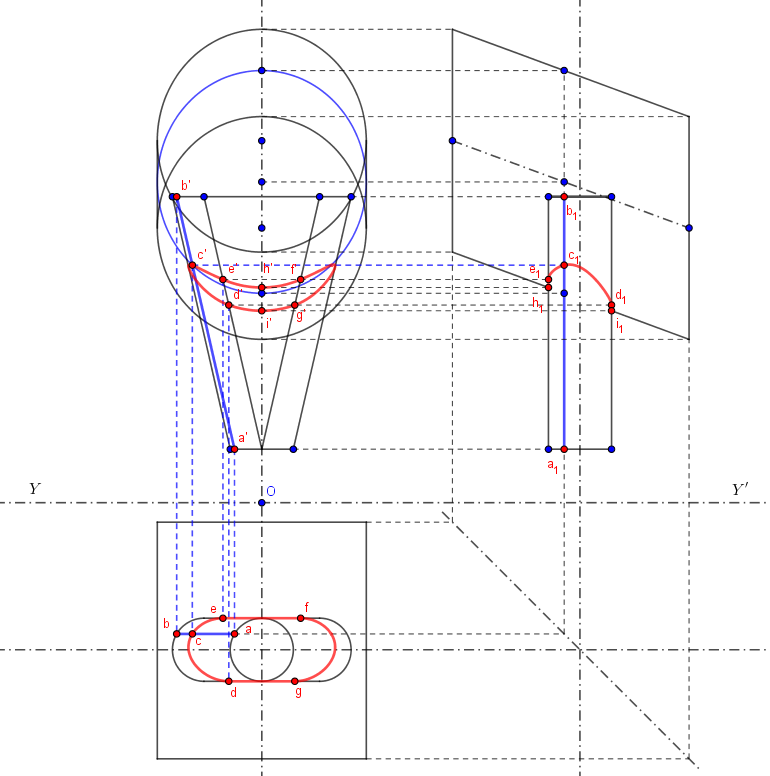
Ceci est rendu possible parce que Geogebra sait tracer des ellipses et construire des intersections droites/ellipses mais il faut bien se rendre compte que lorsque le plan frontal auxiliaire balaye la figue, l'ellipse bleue navigue (en restant de "même taille") entre les deux ellipses noires qui limitent le cylindre.

Faire cette construction point par point à la main ... hum, comment dire...

Effectivement, lafol t'a indiqué un lien pour Geogebra: un merveilleux logiciel.

Il est libre et gratuit. Tu peux le télécharger gratuitement. Pour la formation, en général, on se forme tout seul . Il y a tout de même une aide intégrée et le logiciel est très intuitif.

Bonjour Lake et merci,excuse moi je viens de découvrir par hasard ta réponse. Avant tout,ton plan de coupe est il bien perpendiculaire à l'axe du grand cylindre ce qui décrirai  l'ellipse?

Cordialement,

ah,pardon,je n'avais pas vu tout de suite ton plan de coupe parallèle au plan de projection!

Oui, parallèle au plan frontal de projection.

Et sa principale qualité pour la suite des évènements est de contenir une génératrice du demi cylindre de la surface  composée.

D'accord,je fais cela et ensuite on voit pour le développement de la surface composéet si tu veux bien ,mais je pense avoir une petite idée et qu'il faudra retrouver les Vraies. Grandeur des génératrice et procèder par triangulation (v.g generatrices+v.gdiagonales).

Bon dimanche à toi.

Juste un petit rectificatif: j'ai considéré que le grand cylindre était un cylindre de section normale à son axe circulaire en sorte que les sections par un plan auxiliaire frontal étaient des ellipses.

Mais en y regardant de plus près, j'ai repéré sur ta figure de départ le "cylindre à base circulaire". Il semblerait que je me sois compliqué la vie inutilement puisqu'alors les sections par des plans auxiliaires frontaux ne sont pas des ellipses mais des cercles identiques au cercle de la base.

Ça ne change rien quant au principe de l'épure; les constructions sont justes simplifiées.

Re Bonjour Lake,oui effectivement la bases du cylindre est circulaires et donc oui, vu que le plan auxiliaire  est parallèle à la projection  cela genere des cercles ,j'ai vérifié sur ma conception 3 D c'est bien cela.

Cordialement,

Une question avant de commencer,tu utilises la méthode de plans sécant pour tracer les génératrices en vue de dessus?

Cordialement,

Aussi,détermines-tu un système régulier de génératrices?

A vrai dire, je ne me suis pas posé de question:

Ta surface composée est constituée de deux plaques triangulaires parallèles (et parallèles au PF de projection) et de deux demi cylindres qui chacun s'appuient sur deux demi cercles identiques dont les plans sont parallèles (et parallèles au PH de projection).

J'ai considéré que par exemple le demi cylindre de gauche était engendré par des génératrices (projections tracées en bleu) parallèles au PF de projection. Et ça tombe bien: en PH (ou en vue de dessus si tu préfères), on voit bien que les deux demi cercles sont tangents aux deux plaques horizontales donc que le demi cylindre est tangent à ces deux plaques (la droite de contact étant visible sur la PF mais non nomenclaturée: le côté "gauche du triangle).

De toute manière, on était bien obligé de choisir les génératrices parallèles à l'axe du demi cylindre  c'est à dire la droite qui joint les centres des deux demi cercles et donc parallèles au PF de projection.

je ne vois pas comment tu procèdes pour positionner les points e,d,f,g en projection horizontal...Pour la génératrice a,b (bien qu'elle soit position au hasard selon toi)c'est bon et son intersection avec le cercle donne le point c',jusqu'à là no problème,

Ce sont les points limites des différents arcs de la courbe intersection.

Ils correspondent aux deux plans auxiliaires frontaux limites, c'est à dire aux deux plans parallèles des faces planes (les triangles) de la surface composée.

Ces deux plans recoupent le cylindre principal suivant deux cercles qu'il suffit de tracer en PF. Ils recoupent les deux génératrices limites (les côtés du triangle) en quatre points et . Les lignes de rappel donnent , et en PH.

Les arcs de cercle et font partie de l'intersection cherchée.

En ce moment, je ne peux pas me libérer comme je le souhaiterais. Je te réponds comme je peux quand j'ai un peu de temps libre...


  

Une nouvelle figure (avec des cercles cette fois ci).

Les lignes de construction concernées sont en vert.

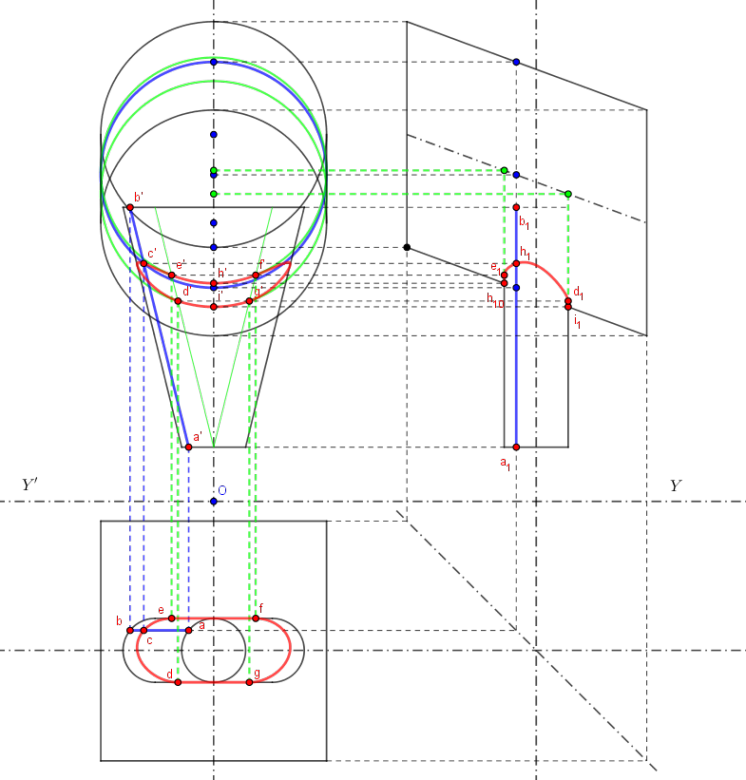
Bonjour,

La suite c'est ce qui est écrit par david1972 le 13-01-19 à 08:25.
Développer la surface composée ne pose pas de gros problèmes, sauf peut-être pour estimer la circonférence des demi-ellipses orthogonales aux génératrices des demi-cylindres, et pour le contour de l'intersection...

Bonjour Lake et merci pour ton temps.ça y est j'ai compris comment tu procédais pour définir les points d',e',f',g' et aussi cela me permet de définir d'autres points et génératrices ne pouvant raccorder les points que  points par points et  ainsi affiner la courbe d'intersection avec mon logiciel CAO/DAO.
Encore merci à toi,excellente journée.

Bien cordialement,

Bonsoir et de rien david1972

Bonjour Lake,
Les points i1 et h10 sont bien les points limite de la courbes d'intersection en vue de gauche et ils sont bien à prendre en considération pour le tracé de la courbe  points par points?

Oui! Geogebra a automatiquement renuméroté ces points en cours de route et je ne m'en suis pas aperçu. Pour une notation plus homogène:

  - (en V de G) correspond au point (en PF) et devrait être noté

  - (en V de G) correspond au point (en PF) et devrait être noté

Avec ces nouvelles notations, en V de G:

   Le segment est la projection de l'arc de cercle et fait partie de l'intersection.

   Le segment est la projection de l'arc de cercle et fait aussi partie de l'intersection.

Pour le développement de cette surface composée,il est peut-être plus juste de rechercher la section normale des  portions de cylindre à base circulaire plutôt que d'opérer par triangulation en recherchant la vraie grandeur des génératrices et diagonales,qu'en penses-tu?
Bonne fin de soirée,

Bonjour,

  Je ne pense rien: il me semble que les méthodes par triangulation (je ne connais pas) donnent des développements approchés réservés aux traçages de chaudronnerie.

  Personnellement, je développerais une section normale à l'axe d'un demi cylindre (d'où des mesures de longueurs d'arcs d'ellipse) et je reporterais des longueurs de génératrices (de chaque côté et perpendiculairement au plan de coupe).

  Mais pour le coup, c'est un peu le logiciel utilisé et ses fonctionnalités qui décident...

  En ce qui concerne Geogebra, on atteint là ses limites: faisable mais trèèès délicat à mettre en œuvre.

Oui,ils utilisent la triangulations quand ils ne peuvent pas faire autrements.

Oui et  dans le cas ou les sommets de la surface sont inaccessible comme tronc de cône par exemple . En revanche, dans certains cas  comme celui d'un raccordement de deux sections parallèles l'une circulaire, l'autre elliptique ou une surface conoïdale, non réglée, ils utilisent la méthode des plans tangents pour définir les génératrices, plus juste que la triangulation(génératrices+diagonales qui en réalité  sont de fausses génératrices et donc en fabrication, particulièrement au cintrage de la pièce , on obtient une pièce gauche…  ,si tu le souhaites je pourrais te fournir des infos plus détaillées dessus. En attendant, j'ai retrouvé un tracé qui me permet de définir l'ellipse en vraie grandeur autrement dit la section normale des portions cylindriques à bases circulaires qui composent cette surface composée.

Bien cordialement,

En tôlerie et chaudronnerie, on obtient le développement de la  surface en référant à la position de la fibre neutre. La position de la  fibre neutre (parti du métal qui ne subit ni allongement ni rétrécissement ) varie en fonction de l'épaisseur et du rayon de pliage de la tôle,en général,pour les grands rayons elle se situe à la moitié de l'épaisseur de la tôle. Pour un pli dont le rayon intérieur est compris entre l'épaisseur et trois fois l'épaisseur du métal on considère que la fibre neutre se situe au tiers de l'épaisseur la tôle en partant de l'intérieur du pli.
Enfin, j'essaie dans le cas ou modélise des pièces développables en tôlerie de tenir compte de cette contrainte de position de fibre et apparemment ils excitent aussi d'autres contraintes qu'apparemment mon logiciel CAO conçu par des tôliers pour des tôliers prend en considération, voilà pour le petit cour. A bientôt,

Merci david1972 pour ces précisions.

Je suis finalement parvenu à faire un développement ("exact") avec Geogebra (et du mal!)

  

Et si on a des doutes, on a aussi quelques petits "contrôles" immédiats:

Bon travail Lake,à moi de jouer!

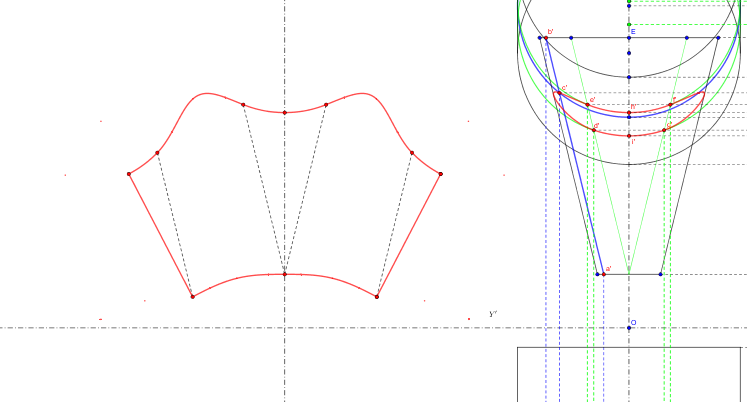
Tout d'abord l'épure qui permet de retrouver la courbe d'intersection entre la surface composée et le volume cylindrique.Également,l'épure (rabattement de la portion cylindrique de la surface composée) qui permet de déterminer les vraies grandeurs des génératrices ainsi que la vraie grandeur de la section normale(elliptique dans ce cas) des portions cylindriques de la surface composées qui sont  nécessaire pour le calcul  développé.Aussi le développement de cette surface composée sans tenir compte,dans un premier de l'intersection avec le volume cylindrique.

Salutation,

Tout va bien
Reste à reporter les longueurs de génératrices.
Bien sûr, tes courbes sur le développement seront moins accentuées que les miennes: j'avais volontairement incliné le cylindre principal sur ses bases pour avoir de « jolies » courbes.

Avec le développement définitif de la surface composée

Nickel!

Bonjour Lake,on pourrait peut-être s'occuper du dernier élément de cet ensemble chaudronnée à savoir l'auge et le capot de fermeture?
Déterminer la pénétration de la surface composé dans l'auge (dont nous avons vu précédemment)et son développement et déterminer la courbe du capot de fermeture et pourquoi pas son développement.

Voilà la suite en capture d'écran.

Pour le développement de l'auge (je pense à la partie percée), c'est exactement la même technique.

Quant au "capot de fermeture", pour l'instant, on ne connait rien de ses caractéristiques

Oui,d'accord pour l'auge,il faut déterminer sa section normale qui devrait-être elliptique vu que le bases sont circulaires et donc les vraies grandeurs des génératrice après les avoir défini sont en projection horizontale.Concernant le capot de fermeture,quelles caractéristiques voudrais-tu?

pardon petite rectification concernant mon post précédant concernant  l'auge, il faut définir les génératrices qui sont en vraies grandeur en projection frontale

De ce que je vois et sans autres précisions, je suis obligé de faire des suppositions:

  - Le capot serait une portion de cylindre.

  - Son axe est orthogonal à celui du cylindre de l'auge.

  - Les deux axes sont-ils sécants ? Je ne pense pas. Je verrais bien son axe au niveau le la face supérieure de l'auge.

En tout état de cause, il faudra réaliser (comme précédemment avec la surface composée) une épure avec les intersections cylindre/capot et cylindre/auge d'une part, cylindre/capot et plans latéraux/auge d'autre part puis effectuer ensuite le développement de l'auge.

De mon côté, je commence à  avoir de grosses difficultés avec mon dessin:
Il y a beaucoup de lignes de construction que je cache pour que les figures soient lisibles et comme je le disais plus haut, GeoGebra commence à atteindre ses limites:

Par exemple (mais pas que cette commande), avec mon dessin, la commande "Afficher/cacher l'objet" met environ 10 secondes pour être effective. Il faut 10 autres secondes pour en sortir. Bref, ça commence à être infernal et je commence à avoir du mal à m'y retrouver. Juste une figure avec toutes les lignes pour que tu te rendes compte:

  

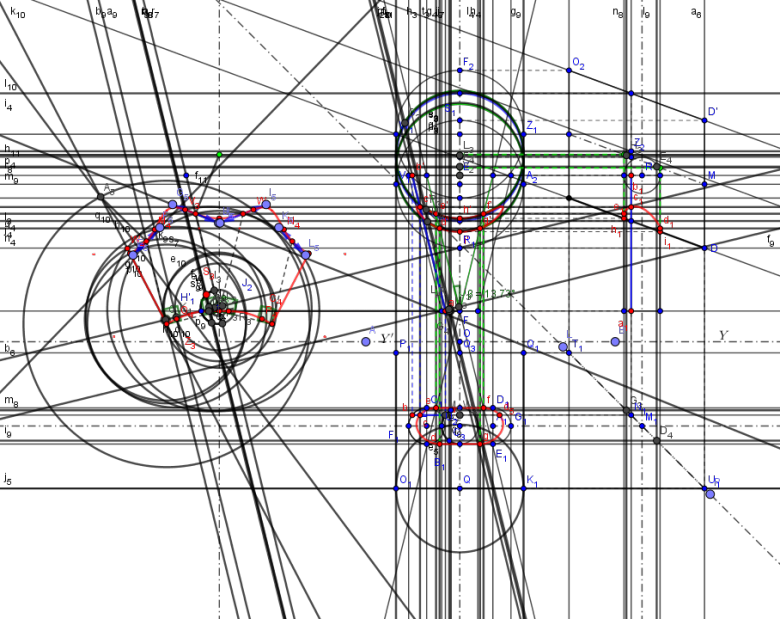
Tout ça pour te dire que je vais avoir des difficultés quasiment insurmontables pour poursuivre de mon côté  avec GeoGebra ...

Voici les cotations de l'ensemble,

Oui,d'accord,pour ma part sur mon logiciel c'est beaucoup plus simple,je n'ai qu'a décoché ce ce je veux caché,c'est immédiat...