Inscription / Connexion Nouveau Sujet
Géométrie dans l'espace
Bonjour, je viens vous demander votre aide pour un exercice auquel j'ai énormément de difficulté, pourriez vous m'aidez? Je ne souhaiterais pas que les réponses mais des aides afin de pouvoir m'améliorer sur ce chapitre et de mieux le comprendre
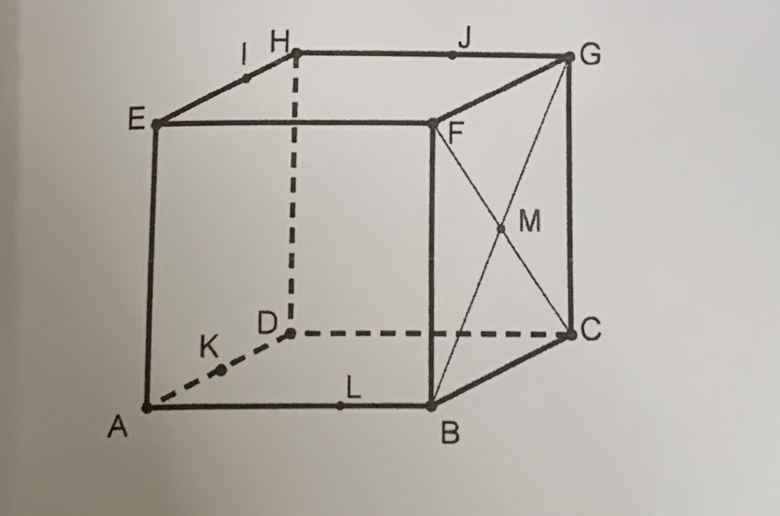
Dans le cube ABCDEFGH ci-dessous, M est le centre de la face BCGF et
Répondre par vrai ou par faux aux propositions suivantes. Justifier votre réponse.
a Les droites (KJ) et (IL) sont sécantes (procéder par l'absurde)
--> Je ne sais pas ce que c'est par l'absurde
b. M appartient au plan (HAB).
c. L'intersection de la droite (HM) et du plan (ABC) appartient au plan (ABE).
d. (HB) et (DF) sont perpendiculaires.
e. La droite (AH) est orthogonale au plan (EFC)
Je vous met ci joint la figure
Merci d'avance pour prendre le temps de m'aider
Bonjour,
"par l'absurde " est le type de raisonnement suivant (en général) :
supposons la propriété P (en général disais-je) vraie
alors (suite du raisonnement ...) on aboutit à une contradiction, une conclusion en opposition avec l'hypothèse
donc la propriété P est fausse.
ici que veut dire dans l'espace que deux droites sont sécantes ? quelle condition nécessaire pour quelles le soient ?
Si je comprends bien l'absurde, cela signifie par exemple que si je di que 1+1=2 et que je trouve après démonstration que 1+1 =3 alors 1+1 ne peut pas être égal à 2?
Deux droites sont sécantes dans l'espace si elles sont coplanaires, c'est à dire qu'elle appartiennent au même plan, est ce bien cela?
c'est l'idée (mais dans cet exemple tu vas avoir du mal à aboutir à 1+1= 3  )
)
oui, c'est une condition nécessaire (mais pas suffisante, car si coplanaires, elles pourraient aussi bien être parallèles)
donc ici si elles sont sécantes, cela implique qu'elles sont coplanaires donc que les points ... sont coplanaires donc ... etc
Oui en effet ici l'idée du 1+1 va être difficile à prouver xd
petite idée :
Supposons que les droites (KJ) et (IL) sont sécantes, alors cela signifie que les droites (KJ) et (IL) sont coplanaires et non parallèle donc que les point K, J , I,L appartiennent au même plan.
Or (KL)// (IJ) car ils appartiennent à deux faces //. Donc les points sont bien coplanaires, ce qui prouvent que les droites sont sécantes
(je pense pas avoir tt juste mais j'ai essaye)
deux droites quelconques de deux plans parallèles ne sont pas forcément parallèles !!
tu affirmes que par exemple les droites (AB) et (FG) seraient parallèles au prétexte qu'elles appartiennent aux deux plans parallèles (ABC) et (EFG) ??
et utiliser un raisonnement par l'absurde c'est pour prouver que la propriété P est fausse, pas qu'elle est vraie !!
Donc à la base je dois supposer que mes droites ne sont pas sécantes donc non coplanaires donc que les points n'appartient pas à la même face et je dois prouver le contraire ?
bein non 
tu supposes qu'elles sont sécantes ...etc (ton début était bon, c'est ensuite que ça se gâte !) tu aboutis à une contradiction, donc elles ne sont pas sécantes.
Supposons que les droites (KJ) et (IL) sont sécantes, alors cela signifie que les droites (KJ) et (IL) sont coplanaires et non parallèle (inutile) donc que les point K, J , I, L appartiennent au même plan.
ça c'est bon
c'est ensuite que ça c'est faux :
Or (KL)// (IJ) car ils appartiennent à deux faces // Donc les points sont bien coplanaires
c'est sur que si les points sont coplanaires, les points sont coplanaires et on ne prouve rien du tout ni dans un sens ni dans l'autre ! (raisonnement qui tourne en rond dans un cercle vicieux)
la suite correcte pourrait être
donc (KL)// (IJ) sont parallèles car intersections du plan (IJKL) avec les plan // (ABC) et (EFG)
mais .... (KL) et (IJ) sont elles réellement parallèles ???
c'est là la contradiction cherchée...
Oula a mon cerveau fume
Déjà je voulais te remercier pour l'aide que tu m'apportes car je sais que ça te prends du temps et beaucoup sûr de patience pour tt m expliquer.
(EF) // (AB) et (FG)//((BC) donc les plans (ABC) et (EFG) sont parallèles ce qui signifie que tt droites contenue dans l'un est parallèle au plan qui lui est parallèle c'est pas ça?
(EF) // (AB) et (FG)//((BC) donc les plans (ABC) et (EFG) sont parallèles oui.
toute droites contenue dans l'un est parallèle au plan qui lui est parallèle oui
mais ça ne veut pas dire parallèle à toute droite de ce plan !! ça c'est faux
de toute façon on n'a pas besoin de ça ici :
faut il vraiment démontrer des détails du genre "je prouve explicitement que les plans (ABC) et (EFG) sont parallèles en partant de la seule et unique hypothèse que les faces du cube sont des carrés" ??
à un moment il faut s'arrêter dans le formalisme à outrance sous peine d'avoir des démonstrations totalement illisibles, perdues dans des détails "évidents" qui ne font que obscurcir le cheminement global de la démonstration :
hypothèse (KJ) et (IL) sécantes
donc coplanaires, donc les points I,J,K,L coplanaires donc les intersections (IJ) et(KL) de ce plan avec les plans parallèles (ABC) et (EFG) sont parallèles
on en est là : (IJ) // (KL)
et la question est "est-ce vrai ?"
visiblement non :
la parallèle à (KL) passant par I est la droite Δ qui n'est pas la droite (IJ) !
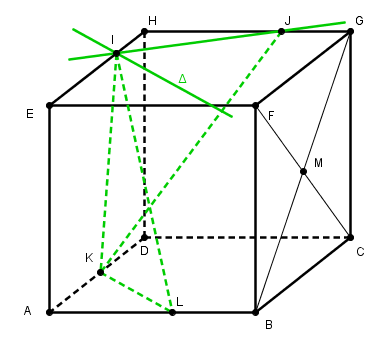
et c'est terminée
on est arrivé à une contradiction : les droites (IJ) et (KL) sont à la fois parallèles et non parallèles !
donc l'hypothèse de départ est fausse et les droites (KJ) et (IL) ne sont pas sécantes
la propriété (a) est fausse terminé
(on ne te demande pas de prouver la propriété (a) mais de dire si elle est vraie ou fausse !!)
Merci beaucoup en tout cas car c'est vraiment pas évident pour moi et il est vrai que je me trompe encore pas mal dans les démonstrations dans ce chapitre.
Pour le 2), j'aurais mi vrai car m est le milieu de [GB] et que [AH]// [GB]
Pour la 3) ce que je sais c'est que la position relative entre une droite et un plan , c'est soit ils sont sécantes en un point , soit parallèle soit inclus
On doit commencer par trouver l'intersection de (HM) et (ABC) qui selon moi est le point M car il appartient à (HAB) est ce que le début de mon raisonnement est juste?
parce que tu penses vraiment que M fait partie du plan (ABC) ???
c'est trivialement faux , y a qu'à juste ouvrir les yeux sur la figure !!
indice :
on utilise la question b qui va donner un plan dans lequel se trouve la droite (HM)
et on s'intéresse à l'intersection de ce plan avec (ABC)
ça donnera une construction effective de l'intersection de la droite (HM) avec le plan (ABC)
et la conclusion en découlera
D après la question 2 M appartient à (HAB) donc(HM) appartient à (HAB)
L'intersection de (HAB) et du plan (ABC) est la droite (AB) donc affirmation vrai
L'intersection de (HAB) et du plan (ABC) est la droite (AB)
oui
mais il en manque un gros bout avant d'aboutir à :
donc affirmation vrai
vu que c'est ça la question :
L'intersection de la droite (HM) et du plan (ABC) appartient au plan (ABE).
Pour la 3, je vois pas vraiment mais j'ai pu avancer sur les deux dernières
la 4) Deux droites de l'espace sont orthogonales lorsque leurs parallèles passant par un point quelquonque sont perpendiculaires.... je connais ce théorème mais jeu bloque ensuite
question 5
La droite (AH) est orthogonale à (EFC) si et seulement si elle est orthogonale à deux droites sécantes de ce plan
Or, la droite (AH) est orthogonale à (FC) et ......(je sèche)
Est ce que mes propriétés sont justes?
c) L'intersection de (HAB) et du plan (ABC) est la droite (AB) OK
il faut maintenant faire le lien avec la question qui parle de (HM) et du plan et du plan (ABE) !!
L'intersection de (HAB) et du plan (ABC) est la droite (AB) OK
donc l'intersection de (HM) avec le plan (ABC) (c'est de ça dont parle l'énoncé !!) est le point ???
(faire la figure !!!)
or ce point appartient à quelle droite (!!) qui est incluse dans le plan ... (ABE) !!
d) inutile de parler de parallèles car ces deux droites sont déja dans un même plan (le colorier sur une figute) !!
c'est donc de la pure géométrie plane : les diagonales de ??? se coupent elles à angle droit ou pas ?
faire la figure en vraie grandeur de ce plan
e) oui
pareil, dessiner ça explicitement, la figure donnera des idées ...
(la trace complète du plan (EFC) sur les faces du cube, colorier ce plan)
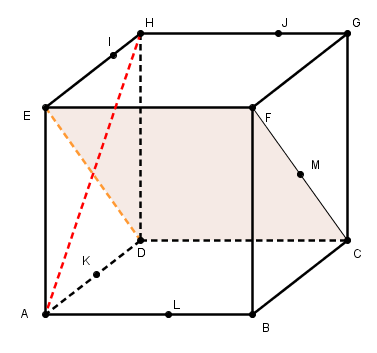
"Or, la droite (AH) est orthogonale à (FC)" ou plus simple : orthogonale à (ED) (elle y est même carrément perpendiculaire, c'est de la géométrie plane dans (ADH)
une autre droite sera par exemple la droite (EF) car c'est une arête du cube donc othogonale au plan (???)
3) l'intersection de (HM) avec le plan (ABC) Est le point F qui lui est inclus dans le plan (ABE)
Donc affirmation vrai?
HB et DF sont les diagonales du parallèlogramme HBDF. Les diagonales d'un parallélogramme ne se coupe pas en formant un angle droit hormis pour le carré et le losange, ce qui n'est pas le cas ici
Affirmation fausse
c) ... avec le plan (ABC) Est le point F
ça ne risque pas, vu que F n'appartient évidemment pas au plan (ABC) = la face ABCD du cube !!
il faut considérer ce qu'il se passe dans le plan (HAB) :
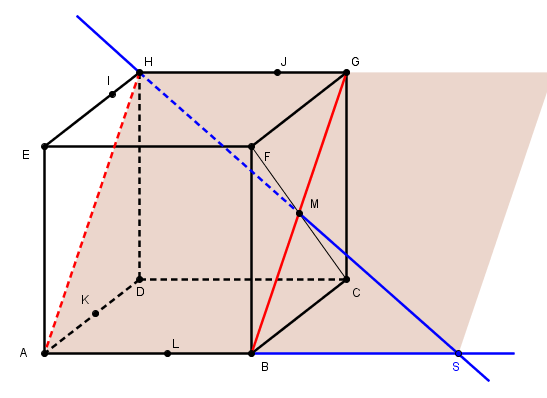
dans ce plan qui contient les deux droites (HM) et (AB) ...
d) oui tout à fait
HBDF est un rectangle qui n'est pas un carré car le coté HF est > HD
(diagonale d'une face du cube est > à son arête)
Je te remercie vraiment pour tout le temps que tu ma consacre . Merci énormément je t'en suis très reconnaissant
Ta 1ère question, ou quasiment, c'était : c'est quoi des droites sécantes.
Sécantes, Sécateur, c'est la même racine. 2 droites sécantes c'est 2 droites qui se coupent.
Voilà, tu n'oublieras plus jamais.
*** heu ... c'est un peu jouer la mouche du coche en disant cela bien après la bataille alors que l'exo est terminé
et que rien ne permettait de supposer que lapinou575757 aurait quelque difficulté que ce soit à comprendre ce mot...
tu fais ça déja plusieurs fois, évite de mettre des contributions aussi inutiles à l'avenir.
modération ***


