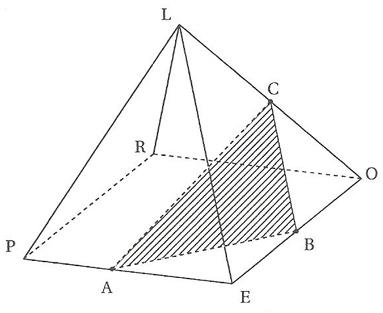
Bonjour, le début est simple, Dans l'intersection il y a déjà le point A donc les deux plans se coupent.

Après, c'est un peu plus dur car il faut un peu d'intuition et trouver une second point d'intersection.
Appelle D le milieu de PL. AD qui est la droite des milieux dans le triangle PEL est parallèle à LE. CB aussi est parallèle à LE (c'est la droite des milieux du triangle OEL. donc CB est parallèle à AD. Comme CB est dans le plan ABC et que AD est la parallèle à BC mené de A qui est également dans ABC, AD est dans ABC aussi. Donc le point D est dans le plan ABC. Il est aussi dans le plan PEL donc il fait partie de l'intersection des deux plans ABC et PEL. Et donc la droite d'intersection des deux plans, c'est AD.

Encore merci de ton aide tu me sauve la vie. Mais quel théorème on pourrait utiliser pour justifier le tracer de l'intersection ?

Juste que l'intersection de deux plans est une droite, que A et D sont dans cette intersection donc que cette droite est forcement la droite AD.

merci. Et euh quand je trace la droite AD, elle n'est pas parallèle à la droite CB. C'est normal

ha si, un dessin en perspective conserve les parallèles, donc ça n'est pas normal. Quoique les hachures faussent un peu la perception. Par exemple CB est parallèle à LE sur le dessin.

bonjour
glapion : on ne pourrait pas utiliser le th. du toit pour justifier?
avec le th. des milieux dans LEO : (BC) coupe (LE) en son milieu
(PLE) et (ABC) contiennent des dtes parallèles : (LE) et (BC).
leur intersection est 1 dte qui leur est parallèle: on trace la parallèle à (LE) passant par A
non?

Je pence qu'il faut utiliser le th du toit. Mais pour la droite AD, D ne sera pas le milieu de LP sinon elle n'est pas parallèle aux deux autres droites.

Oui valparaiso, ça semble une bonne démonstration. Par contre misspoulette, je ne comprends pas bien ce que tu dis. la parallèle à (LE) passant par A c'est AD avec D milieu de (LE) et elle est parallèle aux deux autres droites. La démonstration de Valparaiso est un raccourci mais il arrive à la même conclusion.

Ah d'accord je me suis trompée désolé x]

merci Glapion de confirmer