Inscription / Connexion Nouveau Sujet
Géométrie dans l'espace - Sections
 Tulipe18
Tulipe18Bonjour,
J'ai besoin d'aide concernant cet exercice. En fait, je ne comprends rien quand il s'agit de sections dans la géométrie dans l'espace. Je n'arrive pas à imaginer.
Voici l'énoncé:
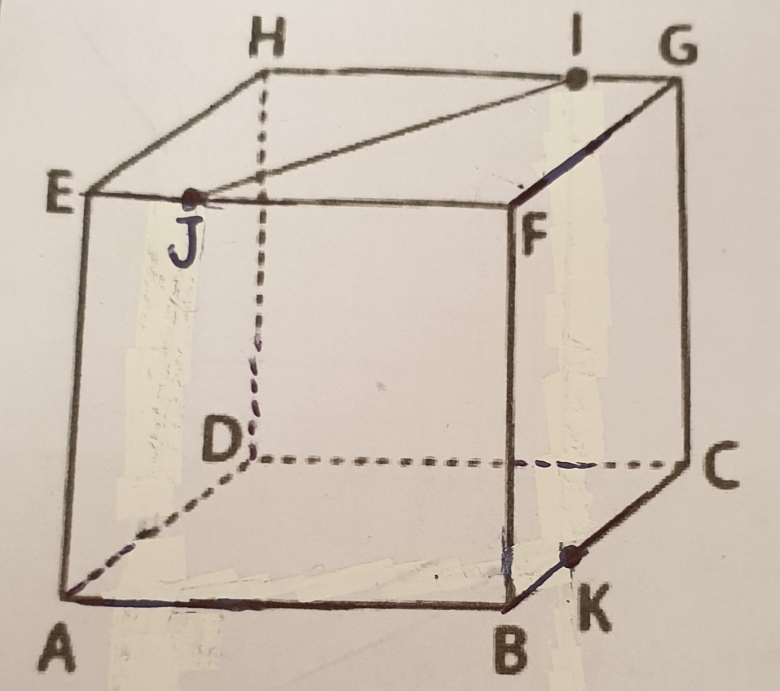
ABCDEFGH est un cube. I est sur [GH]. J est sur [EF]. K est sur [BC].
(Ci-joint le schéma).
Construire la section du cube par le plan (IJK) (on notera si besoin des nouveaux points sur la figure et on citera les résultats de cours utilisés pour obtenir la section).
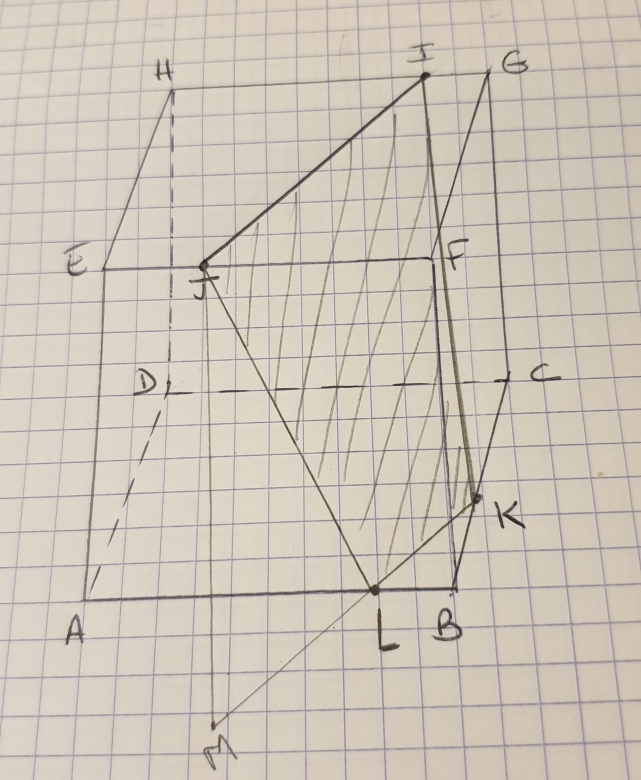
Ci-joint ma construction: la partie hachurée représente (pour moi) la section demandée.
J'ai commencé par dessiner le parallélogramme (JIKN) comme sur mon schéma. Il coupe le cube en J, I, K, L et M (J'ai rajouté les points L et M qui appartiennent à [AB].
Je sais que j'ai fait n'importe quoi, mais je ne vois vraiment pas comment faire autrement, ni comment utiliser mon cours.
Merci pour votre aide
Bonjour
et alors le segment [JL], il appartient pas au plan ?
commence plutôt par prolonger [JI] en une droite et note son intersection avec (FG)
Bonjour,
JN n'étant absolument pas dans le plan (ABFE) ne risque pas de couper l'arête [AB]
ton point M est une pure illusion due à la perspective
nota : la recherche de l'intersection de (JI) avec (FG) est même inutile :
tracer des parallèles suffit car c'est un cube, et donc inutile de lancer la grosse artillerie qui serait nécessaire si les faces n'étaient pas parallèles.
.. à moins qu'on ne veuille faire la construction à la règle (non graduée ) seule
(pas de compas ni d'équerre pour tracer des parallèles)
je partais de ce principe, et puis ce n'est pas une si grosse artillerie, je dirais même que c'est moins fastidieux que de tracer les deux parallèles
Désolé mais je n'ai rien compris : à quoi me sert de prolonger (IJ)? Et quand je trouve le point d'intersection avec (FG) j'en fait quoi?
Par contre, je suis bien d'accord que M ne soit pas dans ABFE car j'essaie d'imaginer cette coupe et si (JM) est parallèle à (IK) alors le point M est décalé par rapport à [AB]. Mais je ne sais pas comment faire.
Merci de m'expliquer comme pour un débutant car la géométrie dans l'espace me pose vraiment problème
Tu n's pas représenté la totalité de la section. Le segment IK est en effet à l'intérieur du cube, et non à sa surface.
Par ailleurs, comment as-tu obtenu le point L ?
En faisant le parallélogramme JIKM. Et comme [JM] est en dehors du cube, j'ai pris que le segment [KL] inclus dans [KM]. Par contre [JM] est dans le cube donc j'ai joins J à L.
Ce n'est pas ça?
Autrement dit, tu as tracé la droite KM parallèle à IJ, qui coupe AB en L. Est-ce bien ainsi que tu as procédé ?
L'intersection de (IJ) et (GF) a plusieurs particularités intéressantes (je le note P maintenant car tous les autres noms sont pris)
-P appartient à (GF) donc à la face GFBC, or K également, donc [PK] est sur la face GFBC
-[PK] est sur le plan (IJK) puisque P et K le sont (P appartient à (IJ))
pas tout à fait, puisque P forme une pointe qui dépasse du cube. Mais le point P te permettrait de placer un autre point Q sur [GC] qui lui est important, puisque la section finale ferait : IJQKL
Zormuche
Oui c'est ce que j'ai finalement trouvé. Mais mon problème avec la géométrie dans l'espace, est que ça ne me vient pas à l'idée de prolonger les droites pour trouver les points d'intersections et donc les segments qui sont inclus dans les plans. Je me contente toujours de mon parallélogramme et de prendre de qu'il y a dans le cube.
Y a t-il une astuce pour penser à prolonger les droites? ou des questions à se poser?
Pour (on citera les résultats de cours utilisés pour obtenir la section) je me contente de ça:
-P appartient à (GF) donc à la face GFBC, or K également, donc [PK] est sur la face GFBC
-[PK] est sur le plan (IJK) puisque P et K le sont (P appartient à (IJ) ?
En tous les cas, merci pour votre aide.
Bonjour,
Je suis assez d'accord avec mathafou :
nota : la recherche de l'intersection de (JI) avec (FG) est même inutile :
tracer des parallèles suffit car c'est un cube, et donc inutile de lancer la grosse artillerie qui serait nécessaire si les faces n'étaient pas parallèles.

@Tulipe18,
On ne voit toujours pas d'où sort le point M.
Pour savoir quel segment prolonger :
Au départ, on ne peut prolonger que le segment [IJ]. On essaye en partant de I puis de J.
C'est plus mieux de I.
Une fois trouvé les points JIQK, on peut prolonger [IJ] à partir de J ou [QK] à partir de K.
"On ne voit toujours pas d'où sort le point M"
le point M est un point qui permet de tracer la parallèle à (IJ) passant par K "à la règle et au compas", méthode classique pour tracer des parallèles ...
c'est dit dès le début mais on aurait aimé une justification explicite de pourquoi on trace cette parallèle
et il ne sert qu'à ça
par contre il est totalement inutile (et même piégeux, la preuve les idées fausses du début) de tracer effectivement ce parallélogramme : les segments [JM] et [IK] ne servent absolument à rien du tout, à part induire en erreur
on veut la parallèle et rien d'autre
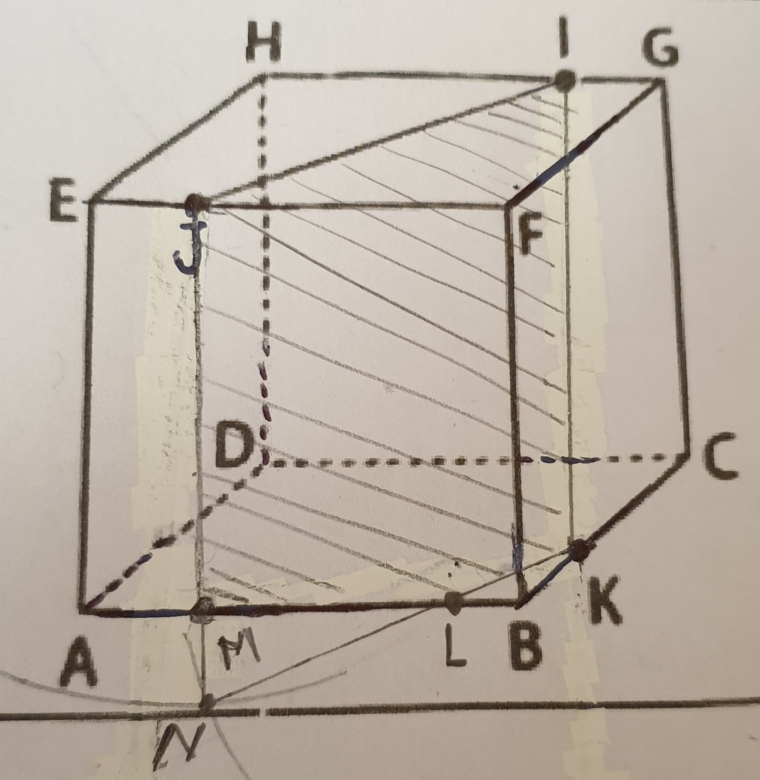
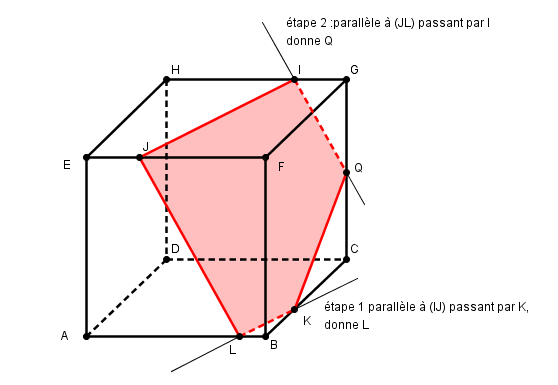
cela est justifié par le théorème :
l'intersection d'un plan (IJK) avec deux plans parallèles (ABC) et (EFG) est deux droites parallèles
on connait l'une d'elles (IJ) et un point de l'autre (K) et donc on peut tracer cette parallèle, ce qui donne L
dans le même esprit :
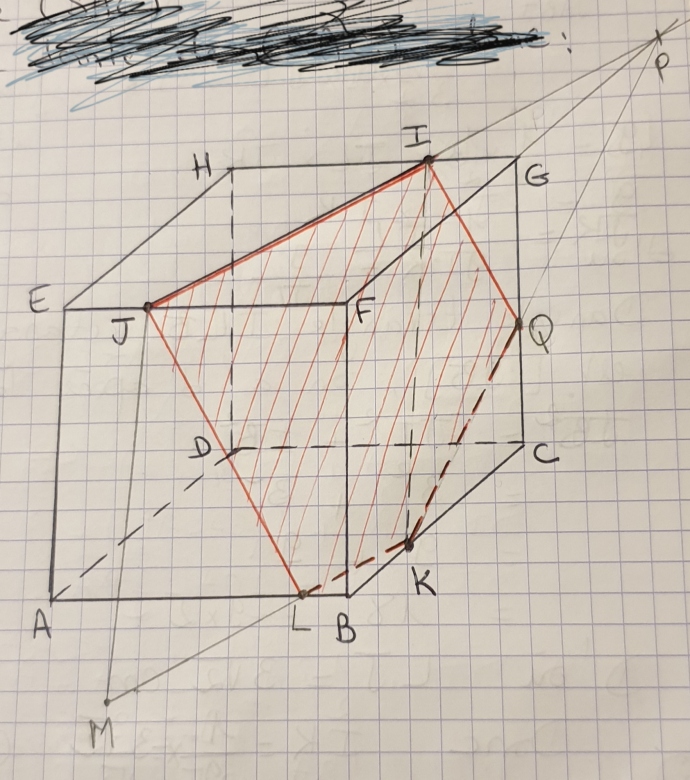
maintenant qu'on connait (JL) du plan (ABE) on peut faire pareil avec les plans (ABE) et (CDG), faces avant et arrière du cube, ce qui donnera Q sans faire intervenir l'intersection P de (IJ) et (CG)
à l'inverse, on peut tout faire sans aucune parallèle :
Une fois trouvé les points JIQK, on peut prolonger [IJ] à partir de J (inutile et déja fait la droite (IJ) est déja tracée) ou [QK] à partir de K en la droite (QK).
et son intersection avec la droite (BF) etc :
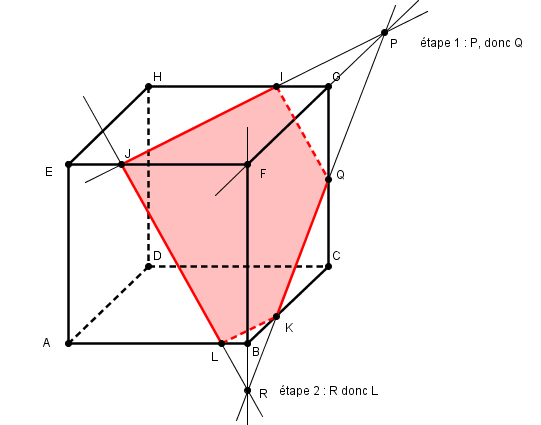
cette construction à l'avantage
• d'être plus intéressante (chercher des points d'intersections de droites et plans divers)
• d'être au final plus simple car on ne trace que des droites avec la seule règle au lieu de parallèles plus compliquées à tracer (usage du compas ou de l'équerre)
• de fonctionner même si ce n'est pas un cube (faces non parallèles )
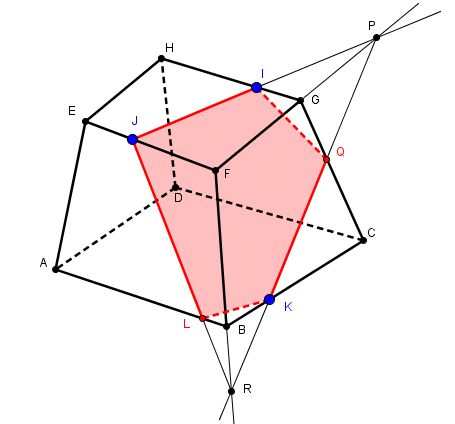
(nota : les 8 points ANCDEFGH ne sont pas tous quelconques car les faces doivent être planes)
il faut bien un inconvénient à tous ces avantages :
un peu plus d'imagination et de "vision dans l'espace" pour identifier les bonnes droites et plan ...
Bonsoir,
Merci mathafou, j'ai fini par comprendre d'où sortait le point M :
le point M est un point qui permet de tracer la parallèle à (IJ) passant par K "à la règle et au compas", méthode classique pour tracer des parallèles ...
Quand j'ai écrit "on peut prolonger [IJ] à partir de J ou [QK] à partir de K.", c'était dans le but de montrer à Tulipe18 qu'il fallait essayer ou imaginer et choisir ce qui permet d'avancer.
Bravo pour les figures. Avec les étapes numérotées, c'est très clair

sur la figure du tout premier message de la discussion le point M s'appelait N et était visiblement construit par intersection d'arcs de cercles pour construire le parallélogramme cité dans le texte de ce premier message.