Inscription / Connexion Nouveau Sujet
Géométrie dans lespace
Bonjour qui pourrait m'aider sur un exercice de géométrie dans l'espace en lava
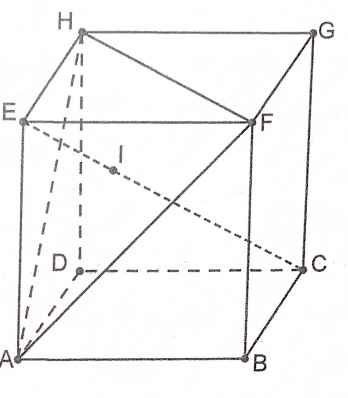
On considère le cube ci-contre, d'arête 1.
a. Montrer que la droite (EC) est
orthogonale au plan (AFH).
Je pense qu il faut montrer que (Ec) est orthogonale à deux droites sécantes du plan c'est à dire (AF) et (AH) mais je ne sais pas comment
b. Soit Ile point d'intersection de (EC) et
(AFH). Calculer la hauteur El du tétraèdre
EAFH.
-> la je suis bloqué
Figure:
Merci de votre lecture et de votre aide
Bonjour,
pour la 1ère question, je calculerais les coordonnées de vecteurs dans un repère orthonormé d'origine E, puis je calculerais leur produit scalaire.
Écris ce que tu auras essayé stp.
Cordialement,
--
Mateo.
Bonjour,
On peut aussi utiliser les milieux J et K de [HF] et [GC] pour démontrer que (EC) est perpendiculaire à (HF).
Puis démontrer de même pour (AF).
Bonjour et merci de vos aides
Je n'ai pas vu les coordonnées de vecteur dans l'espace ni les produits scalaires donc il m'est impossible de passer par cette méthode.
Bonjour,
On peut aussi utiliser les milieux J et K de [HF] et [GC] pour démontrer que (EC) est perpendiculaire à (HF).
Puis démontrer de même pour (AF).
Je vois pas du tout comment il faudrait faire sachant que les points j et k n'existent pas, devrais je les nommer et ensuite
Bonjour,
On peut aussi dire que (EC) est axe de symétrie ternaire du cube en constatant que le triangle AFH est équilaréral et que E comme C sont respectivement à distance 1 et  2 des 3 sommets A F et H.
2 des 3 sommets A F et H.
Bonjour vham,
En terminale, ne faudrait-il pas faire intervenir des plans médiateurs ?
Les points E et C sont équidistants de H et F.
La droite (EC) est donc incluse dans le plan médiateur de [HF].
Toutes les droites de ce plan médiateur sont orthogonales à la droite (HF).
Donc les droites (EC) et (HF) sont orthogonales.
De même pour les droites (EC) et (AF).
Bonjour Sylvieg,
Votre raisonnement est bien sûr impeccable.
Je pensais juste attirer l'attention de lapinou575757 su la symétrie ternaire du cube suivant une grande diagonale (EC), puisqu'il avait placé un point I sur lequel il commençait à penser...


