Inscription / Connexion Nouveau Sujet
1)
a)
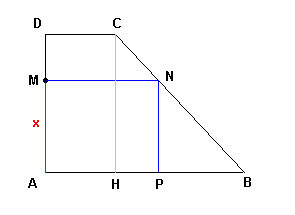
Angle(CHB) = 90°
CH = AD = 4
HB = AB - CD = 6 - 2 = 4
--> CH = HB
Le triangle BCH est donc isocèle rectangle en H
---
b)
Les triangles BCH et BNP ont leurs cotés respectifs sur des droites parallèles ou confondues.
--> ces 2 triangles ont leurs angles égaux 2 à 2
Les triangles BCH et BNP sont donc semblables (de même forme)
--> Comme le triangle BCH est isocèle rectangle en H, le triangle BNP est isocèle rectangle en P.
---
c)
AM = NP comme coté opposés du rectangle AMNP
NP = PB puisque le triangle BNP est isocèle rectangle en P.
--> AM = PB = x
-----
2)
AP = AB - PB
AP = 6 - x
Aire(AMNP) = AM * AP
Aire(AMNP) = x(6-x) = 6x - x²
-----
3)
Aire(AMB) = (1/2) * AB * AM
Aire(AMB) = (1/2) * 6 * x
Aire(AMB) = 3x
Aire(DCM) = (1/2) * DC * DM
Aire(DCM) = (1/2) * 2 * (4-x)
Aire(DCM) = 4-x
Aire(ABCD) = (1/2)*(DC+AB) * AD
Aire(ABCD) = (1/2)*(6+2) * 4
Aire(ABCD) = 16
Aire(CMB) = Aire(ABCD) - Aire(DCM) - Aire(AMB)
Aire(CMB) = 16 - (4-x) - 3x
Aire(CMB) = 16 - 4 + x - 3x
Aire(CMB) = 12 - 2x
-----
Sauf distraction. 
*** message déplacé ***
la FAQ du forum
) :
Annuler
connectez vous