Inscription / Connexion Nouveau Sujet
géométrie descriptive
j'ai le problème suivant
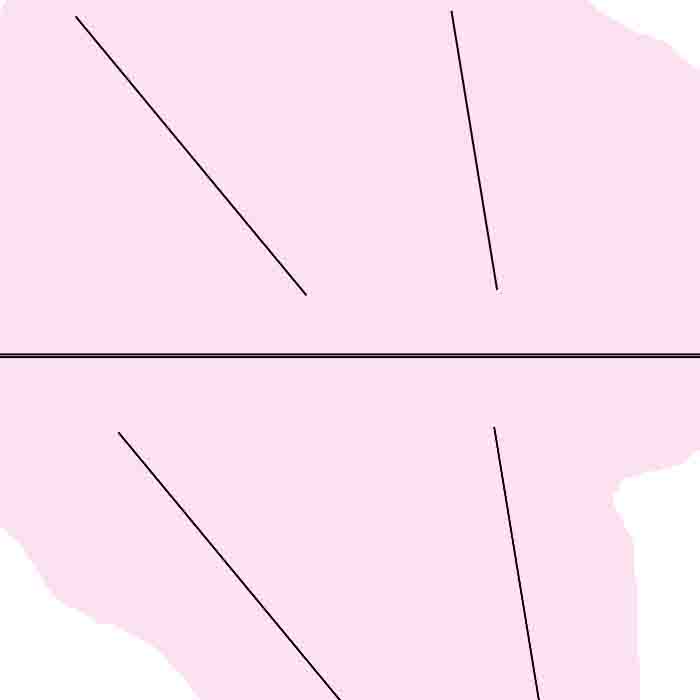
Au dessus de l'horizontal j'ai une droite d inclinée à 45 ° , et parallèle à la m^me droite appelée d' située en dessous de la ligne horizontale.
A côté de cette droite située au dessus de la ligne horizontale, on a une droite h inclinée à 30°, et parallème à la m^me droite appalée h' située au dessous de la ligne horizontale.
Comment reconnaitre si ces droites d et h sont concourantes sans chercher leur point d'intersection qui est hors de l'épure ?
Merci pour vos conseils et votre aide

Bonjour,
Tu devrais poster une image.
Pour cela clique sur l' icône montagne en bas à droite de fenêtre d' édition...
... et lis les instructions.

bonjour,
Si les droites (h) et (d) étaient concourantes, elles le seraient au même point d'abscisse de la ligne horizontale,
que ces droites soient représentées sur le plan horizontal ou sur le plan frontal.
Or (d) et (h) s'intersectent d'un coté, alors que (d') et (h') s'intersectent de l'autre.
...
\
\
\
\
\
\
\
\
___________________________________________
\
\
\
\
\
\
\
l'autre droite se trouve à côté
!
désolé je n'arrive pas à insérer un croquis JPEG m^me si il fait 30 Ko
Bonsoir,
Je te donne le principe:
Tu prends 2 points et
sur la droite
puis 2 points et
sur la droite
Si et
sont coplanaires les droites
et
le sont aussi.
Le point d' intersection de et de
d' une part et celui de
et
d' autre part doivent être sur une même ligne de rappel.
S' ils ne le sont pas, c' est que les droites de départ ne sont pas coplanaires.
Bien entendu, il faut choisir les 4 points de telle sorte que les points d' intersection soient dans la limite de l' épure.

j'ai réussi à insérer mon document. Je pense que ce sera plus facile pour m'aider avec l'épure qui en document joint
je vous rappelle l'énoncé du problème:
deux droites étant données par leurs projections , reconnaitre si ces deux droites son concourantes sans chercher leur point d'intersection qui est lors de l'épure
merci beaucoup
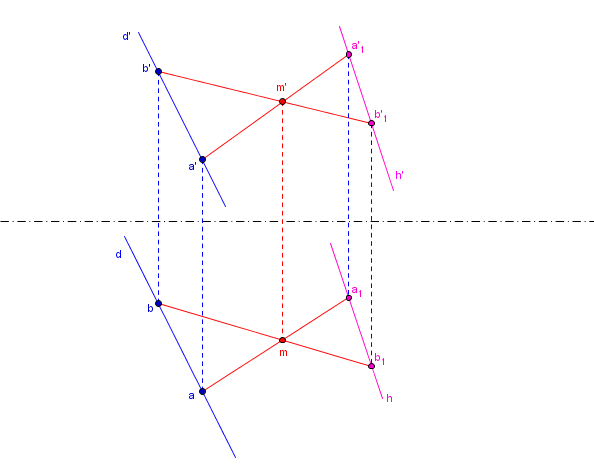
Bonjour,
Ce dessin va avec les commentaires de 23h26.
Les intersections et
sont sur la même ligne de rappel.
Les droites et
sont donc coplanaires et sécantes (car non parallèles).

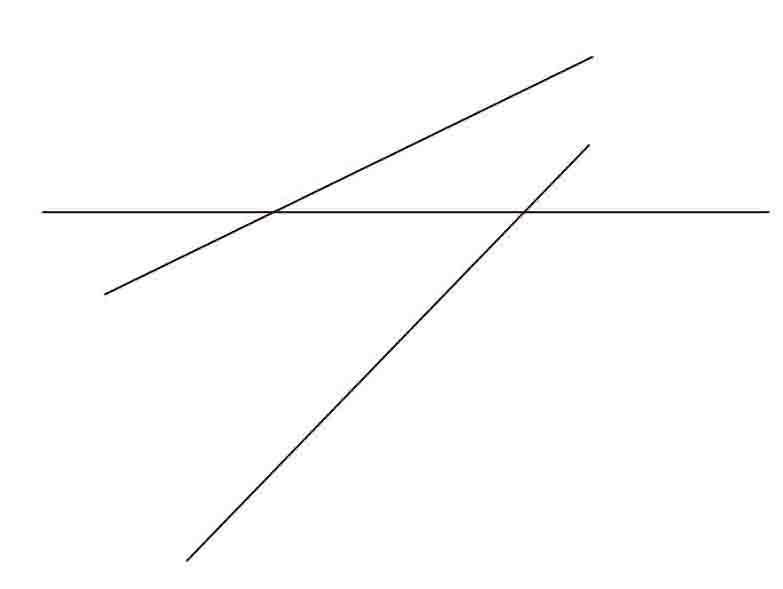
pouvez vous m'aider pour cet exo
une droite D étant donnée par ses projections (dd'), représenter sa symétrie D1 par rapport au plan horizontal de projection
puis sa symétrie:
D2 par rapport au plan frontal
D3 par rapport à la ligne de terre
D4 par rapport au premier bissecteur
D5 par rapport au 2me bissecteur
Re,
Je t' ai répondu dans ton topic ici: ![]() géométrie descriptive
géométrie descriptive
Pour retrouver tes topics une fois connecté, clique sur le petit bonhomme "vos messages" en haut à droite.




 géométrie en post-bac
géométrie en post-bac