Inscription / Connexion Nouveau Sujet
Géométrie et ensembles de points
Bonjour à tous,
je cale sur l'exo suivant :
soit la droite D d'equaion x=-1 et le cercle C de centre(1,0) et de rayon 1.
Une droite delta passant par O coupe D en P et C en Q.
Determiner l'ensemble Gamma decrit par le point M milieu de [P,Q]
---------------------------------------------------------------------
Bon ce que j'ai fait déjà, c'est exprimer les équations des droites et du cercle :
D :  = -1/ cos(
= -1/ cos( )
)
C : 2*cos( )
)
delta :  =
=  0
0
Pour la suite, je ne vois pas comment faire.
A vue de nez,l'ensemble gamma est un cercle, mais je ne vois pas du tout comment procéder.
Merci d'avance pour votre aide
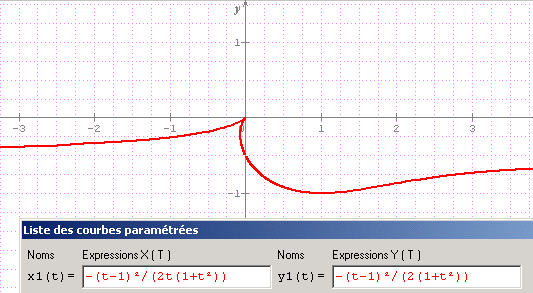
bonsoir
j'obtiens une courbe de cette nature
Philoux
merci pour ta reponse philoux, mais comment je peux prouver ca par le calcul ?
Comment puis-je exprimer les coordonnes du point M en fonction du reste ?
j'ai procédé ainsi, pas en coord polaires :
D : y=ax
C : (x-1)²+y²=1
tu cherches P et Q par intersection D et C :
P( 2/(1+a²) ; 2a/(1+a²) )
Q( -1/a ; -1 )
tu exprimes les coord de I milieu de PQ dont les coord sont fonction de a
xI = -(a-1)²/(2a(1+a²)
yI = -(t-1)²/(2(1+a²)
et j'ai représenter cette courbe en représentation paramétrique
ce n'est peu être pas ce que l'on attend, mais c'est la façon qui m'a semblée la plus accessible.
EN polaire, on doit obtenir des relation rho(théta) plus simples.
A voir... par d'autres car je quitte l'ile 
Philoux
Bonsoir,
Soit P un point de la droite D, (-1,-t) sa coordonnée.
La droite delta a pour équation y=t.x
Le cercle : (x-1)²+y²=1
Donc les points d'intersection du cercle et de delta : (x-1)²+t²x²=1=>x=0 ou x=2/(1+t²)
Q a donc pour coordonnée (2/(1+t²),2t/(1+t²) )
M a donc pour coordonnée (x,y)=
![]()
à vérifier
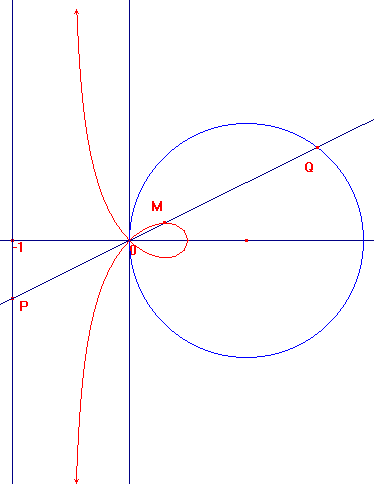
Bien vu caylus !
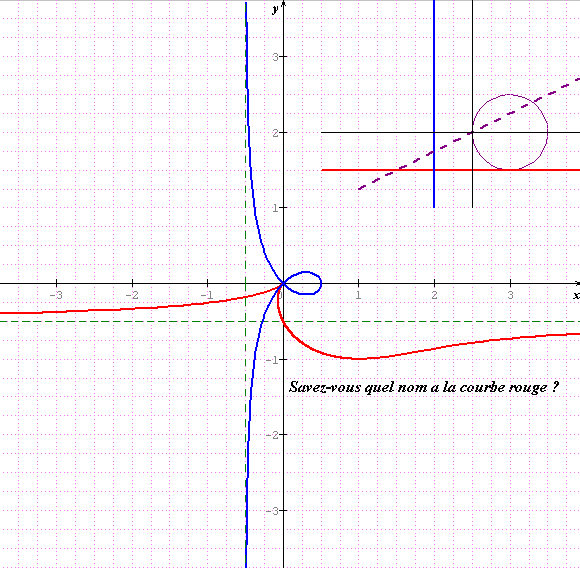
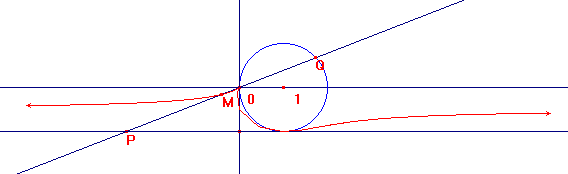
J'ai, en fait, répondu à l'énoncé où c'est y qui vaut -1 :
Bonjour à tous,
je cale sur l'exo suivant :
soit la droite D d'equaion y=-1 et le cercle C de centre(1,0) et de rayon 1.
Une droite delta passant par O coupe D en P et C en Q.
Determiner l'ensemble Gamma decrit par le point M milieu de [P,Q]
---------------------------------------------------------------------
Philoux


 géométrie en post-bac
géométrie en post-bac