Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup GéométrieTopics traitant de géométrie [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

Géométrie Plane

Posté par
DalilaB 01-01-16 à 20:23

Bonjour,

J'ai un problème avec cette exercice de géométrie plane je ne le comprend vraiment pas, merci de votre aide.


Soit ABC un triangle, on note rA, rB, rC les rotations de centre respectif A, B et C et de même angle / 2 .
     1) Démontrer que rCorBorA est une symétrie centrale.
     2) One note I le milieu de [BC]. Comment doit être le triangle ABC pour que le centre de cette symétrie soit le milieu de [BI] ? Faire une figure.

Posté par
carpediemre : Géométrie Plane 01-01-16 à 20:47

salut

calcule l'image des points A, B et C ...

Posté par
DalilaBre : Géométrie Plane 01-01-16 à 21:13

Ah oui j'avais pas pensé a faire ça, merci.

Posté par
alb12re : Géométrie Plane 01-01-16 à 21:34

salut,
comment la composee de 3 rotations d'angle pi/2 peut-elle donner une symetrie centrale ?

Posté par
ThierryPomare : Géométrie Plane 01-01-16 à 22:16

Bonsoir,

Bien entendu, il s'agit de trois rotations du plan affine d'angles de mêmes mesures \pi/3 modulo 2\,\pi.

Bonne soirée !

Posté par
lakere : Géométrie Plane 02-01-16 à 12:01

Bonjour,

Avec des angles de mesure \dfrac{\pi}{3}:

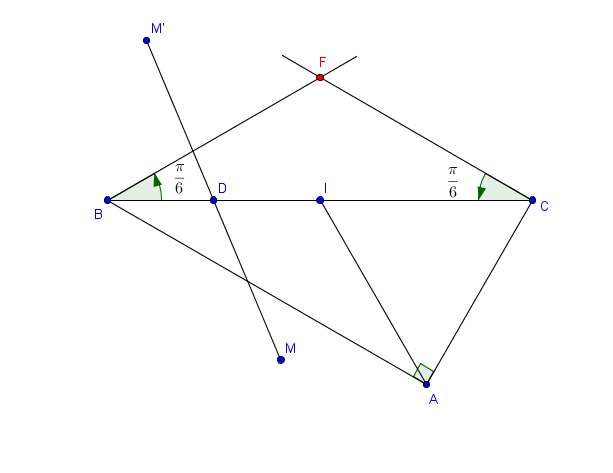
Géométrie Plane

r_B\circ r_C est une rotation d' angle \dfrac{2\pi}{3}

Son centre F est construit sur la figure. (La construction du centre de la composée de 2 rotations de centres différents est un classique ?)

Posons  r_F=r_B\circ r_C

On doit donc avoir:
(r_A\circ r_B\circ r_C)(B)=I

soit (r_A\circ r_F)(B)=I

    r_A(C)=I

A est donc le point tel que IAC soit équilatéral direct.

Posté par
lakere : Géométrie Plane 02-01-16 à 12:09

De toute façon construire le point F est un luxe:

Il est clair que (r_B\circ r_C)(B)=C

Posté par
DalilaBre : Géométrie Plane 02-01-16 à 15:08

Oui effectivement c'est / 3 excusez moi j'ai mal recopier.

Par conte je suis completement perdu j'ai vraiment du mal avec cet exercice. Quelqu'un peut m'expliquer le raisonnement s'il vous plait parce que j'aimerais comprendre comment vous avez fait, merci.

Posté par
ThierryPomare : Géométrie Plane 02-01-16 à 15:18

Bonjour,

Les \R-espaces vectoriels \C et \R^2 sont isomorphes. Plaçons nous dans le \R-espace affine \C. Soit A(z_A), B(z_B) et C(z_C). Quelles sont les expressions des rotations affines r_A, r_B et r_C ?

Posté par
DalilaBre : Géométrie Plane 03-01-16 à 15:46

Je sais pas ..
Je bloque réelement sur ce chapitre, j'ai regardé dans mon cours mais je ne trouve pas.

Posté par
DalilaBre : Géométrie Plane 03-01-16 à 16:28

Quelqu'un peut m'expliquer cet exercice dans son ensemble ?

Posté par
lakere : Géométrie Plane 03-01-16 à 17:54

1) r_A\circ r_B\circ r_C est une rotation d' angle \dfrac{\pi}{3}+\dfrac{\pi}{3}+\dfrac{\pi}{3}=\pi\;\;[2\pi]

Autrement dit,  r_A\circ r_B\circ r_C  est une symétrie centrale.

Es-tu d' accord avec ça ?

Posté par
DalilaBre : Géométrie Plane 03-01-16 à 18:02

Jusque là oui

Posté par
lakere : Géométrie Plane 03-01-16 à 18:19

2) r_A\circ r_B\circ r_C ayant son centre au milieu de [BI], on a donc:

(r_A\circ r_B\circ r_C)(B)=I (1)

Or r_B\circ r_C(B)=C (regarde le dessin avec le triangle équilatéral Br_C(B)C)

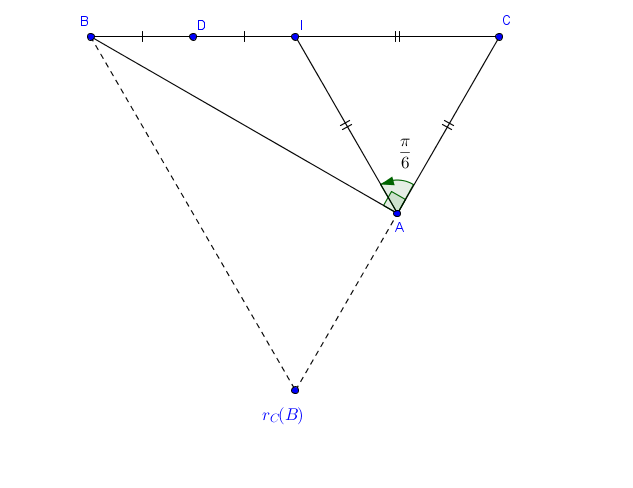
Géométrie Plane

(1) se traduit donc par:

r_A(C)=I

Ce qui signifie que le triangle IAC est équilatéral direct.

Evidemment, on peut passer par les complexes mais en l' occurrence ...

Posté par
DalilaBre : Géométrie Plane 03-01-16 à 18:48

Je pense que j'ai compris mais d'où vient le /6 ?  

Posté par
lakere : Géométrie Plane 03-01-16 à 19:01

Une erreur (dans le dessin)
L' angle vaut \dfrac{\pi}{3}

Posté par
DalilaBre : Géométrie Plane 03-01-16 à 19:07

Ok, je te remercie d'avoir pris du temps pour m'expliquer , maintenant j'ai compris. Merci encore.  

Posté par
ThierryPomare : Géométrie Plane 03-01-16 à 19:09

Bonsoir,

Posant M'=r_P(M), avec P\in\{A,\,B,\,C\} et M(z) et M'(z'), l'on avait

z'=z_A+e^{i\,\pi/3}\,(z-z_A)
z'=z_B+e^{i\,\pi/3}\,(z-z_B)
et
z'=z_C+e^{i\,\pi/3}\,(z-z_C)

d'où

z'=z_C+e^{i\,\pi/3}\,\left(\left(z_B+e^{i\,\pi/3}\,\left(\left(z_A+e^{i\,\pi/3}\,(z-z_A)\right)-z_B\right)\right)-z_C\right)=\cdots

Bonne soirée !

Posté par
lakere : Géométrie Plane 03-01-16 à 19:09

Posté par
lakere : Géométrie Plane 03-01-16 à 19:29

Moui... Les complexes ici, c' est quand même le marteau pilon pour écraser une mouche


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !