Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Géometrie plane et dans l'espaceTopics traitant de Géometrie plane et dans l'espace [tout]Lister tous les topics de mathématiques

1 2 +

Niveau terminale
Partager :

Géométrie : similitude directe et suite de points

Posté par Profil Fifaliana36 25-08-19 à 17:21

Bonjour.
Dans le plan orienté P,on considère un carré direct ABCD de centre O et AB=\sqrt3cm.
Soit : r la rotation de centre A et d'angle\frac{\pi }{2}
t la translation de vecteur\vec{AB}
et h l'homothétie de centre C et de rapport\frac{-\sqrt3}{3}
1)a) placer G=bar{(D,3),(C,-1)}
b) déterminer et construire les ensembles
()={MP/3MD2-MC2=0}
()={MP/\vec{MC}.\vec{MD}=0}
2) Soit r'=t o r.
a) montrer que r' est une rotation dont on précisera l'angle.
b) Déterminer r'(A) et r'(B). En déduire le centre de r'
3) soit S la transformation définie par S= t o r o h
a) vérifier que S est une similitude directe dont on précisera le rapport n et l'angle
b) Vérifier que S (C)=D.
c) On note I le centre de S. Montrer que I
()()
Placer I
4) Soit (An)n la suite de points définis par :
A0=C
An+1= S(An) , n), n

et (an)n la suite de nbes réels définie par : an= aire du triangle IAnAn+1.
a) montrer, que pour tout n, IAnAn+1 est un triangle rectangle en I, et que (\vec{A_nI},\vec{A_nA_{n+1}})=\frac{\pi }{6}+2k\pi,p.
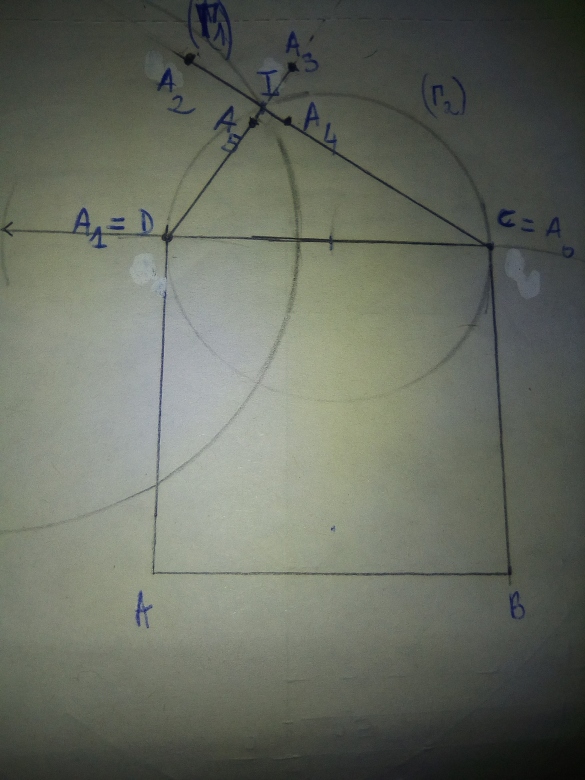
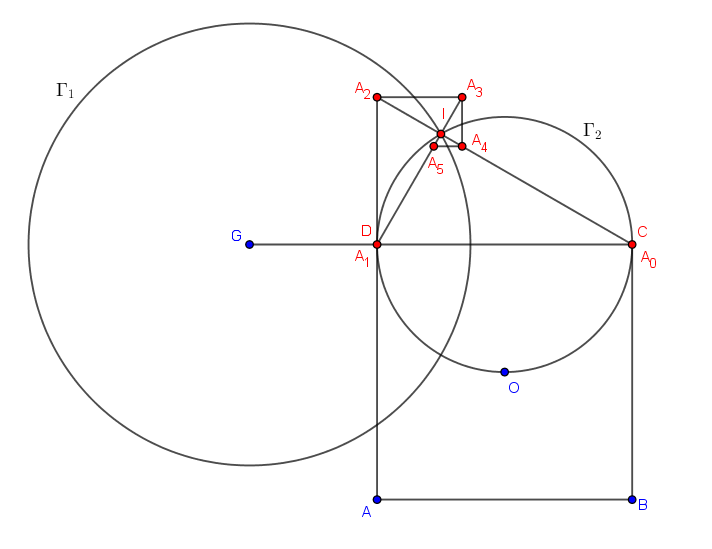
b) placer les pts A0 jusqu'à A5
c) montrer que a_0=\frac{3\sqrt3}{8}\; et\; a_n=\frac{\sqrt3}{6}-(IA_n)^2
d) montrer que la suite(an)n est une suite géométrique et vérifier que :
limn+(a0+a1+...+an)=\frac{9\sqrt3}{16}
Unité d'aire= 1 cm2

Voilà ce que j'ai fait :
1) a)\vec{DG}=\frac{1}2{}\vec{CD}
b)
() est le cercle de centre G et de rayon 3/2.
() est le cercle de diamètre CD privé de C et D.
2) a) j'ai utilisé les propriétés du cours donc r' est une rotation d'angle/2
b) r'(A)=B et r'(B) = C
Donc O est le centre de r'
3) a) j'ai encore utilise les propriétés du cours
Et k=-3/3 et = /2
b) S(C)=D(IC,ID)=/2I() mais je ne sais pas comment monter que I() et pour la suite de points je ne sais pas comment faire.
J'aurais besoin d'aide svp.

Posté par
lakere : Géométrie : similitude directe et suite de points 25-08-19 à 17:47

Bonjour,

Citation :
1) a)\vec{DG}=\frac{1}2{}\vec{CD}


Oui. Il faut le placer sur une figure.

Citation :
b)
   1 est le cercle de centre G et de rayon 3/2.
   2 est le cercle de diamètre CD privé de C et D.


\Gamma_1: un cercle de centre G, oui mais tu as commis une erreur sur le rayon.

\Gamma_2:  Pourquoi diable "privé des points C et D" ?
  

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 25-08-19 à 20:04

Pourquoi c'est pas privé de C et D?

Posté par
lakere : Géométrie : similitude directe et suite de points 25-08-19 à 20:22

Mais pourquoi ça le serait ?

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 25-08-19 à 20:30

Et ben car(2) est l'ensemble des pts M tels que MC.MD=0 c à d (MC,MD)=/2+k. Or ce n'est pas possible pour M=C et M=D , ou bien quelque chose comme ça. Donc j'ai tort ?

Posté par
lakere : Géométrie : similitude directe et suite de points 25-08-19 à 20:49

Si M=C, on a bien:

  \overrightarrow{CC}.\overrightarrow{CD}=0.

Et Si M=D, on a bien:

  \overrightarrow{DC}.\overrightarrow{DD}=0

Non ?

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 25-08-19 à 21:03

Donc CC est perpendiculaire à CD?

Posté par
lakere : Géométrie : similitude directe et suite de points 25-08-19 à 21:31

\overrightarrow{CC} c'est le vecteur nul: \overrightarrow{0}

Et le produit scalaire du vecteur nul avec un vecteur quelconque est nul!

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 26-08-19 à 07:35

D'accord alors2 est le cercle de diamètre CD.
Mais pour2, voilà ce que j'ai trouvé
En utilisant la fonction scalaire de Lebniz,
(M)=3MD2-MC2=0
Or
2MG2+(9/4)-(27/4)=0
2MG2=9/2
MG=3/2

Où est l'erreur ?

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 26-08-19 à 07:36

Désolé c'est1 le deuxième ensemble,

Posté par
lakere : Géométrie : similitude directe et suite de points 26-08-19 à 09:31

Citation :
Or (M)=2MG2+3GD2-GC2=0


C'est juste; c'est ensuite que ça se gâte.

2\,GM^2=GC^2-3GD^2

  GC=\dfrac{9}{2} et GD=\dfrac{3}{2}

  en sorte que 2\,GM^2=\dfrac{27}{2} puis GM=\cdots

Posté par
lakere : Géométrie : similitude directe et suite de points 26-08-19 à 10:42

Je pense qu'il y a des erreurs dans ton énoncé:

  

Citation :
c) montrer que a_0=\frac{3\sqrt3}{8}\; et\; a_n=\frac{\sqrt3}{6}-(IA_n)^2
d) montrer que la suite(an)n est une suite géométrique et vérifier que :
limn+(a0+a1+...+an)=\frac{9\sqrt3}{16}


J'ai obtenu a_0=\dfrac{9\sqrt{3}}{8}

  a_n=\dfrac{\sqrt{3}}{6}{\red\times}IA_n^2

  et la limite \dfrac{27\sqrt{3}}{16}

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 26-08-19 à 20:03

Ah bon ? et dire que c'est vraiment comme ca.

Posté par
lakere : Géométrie : similitude directe et suite de points 27-08-19 à 08:11

Heu... je ne comprends pas ce que tu veux dire

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 27-08-19 à 13:49

Ce que je voulais dire, c'est que c'est bien a0=3√3/8 et an=√3/6-(IAn)² qui est écrit dans le sujet. Il n'y a sûrement pas d'erreur à moins qu'il n'y ait eu une faute de frappe dans le livre, ce qui reste assez improbable.

Posté par
lakere : Géométrie : similitude directe et suite de points 27-08-19 à 14:45

Je suis désolé; j'ai pris au départ un carré de côté 3 et non de \sqrt{3}

Et donc les valeurs de ton énoncé pour a_0 et la limite sont justes.

Par contre, je persiste avec ceci:

  

Citation :
a_n=\dfrac{\sqrt{3}}{6}{\red\times}IA_n^2

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 27-08-19 à 17:57

Bon, nous y reviendrons plus tard.
Pour ce qui est des ensembles de points,
Si c'était\vec{MC}.\vec{MD}= NOMBRE
Alors comment faire ?

Posté par
lakere : Géométrie : similitude directe et suite de points 27-08-19 à 19:50

Soit tu utilises le théorème de la médiane soit (ce qui revient au même) tu fais intervenir le milieu de [CD] avec la relation de Chasles.

Posté par
lakere : Géométrie : similitude directe et suite de points 27-08-19 à 19:56

Et j'ai oublié de préciser que ta réponse au lieu \Gamma_1:

  

Citation :
GM=3/2


était juste (toujours mon erreur sur le côté du carré initial).

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 27-08-19 à 20:19

Oh franchement, j'ai passé deux heures à vérifier et à revérifier ma réponse sur 1 mais bon n'y revenont plus.

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 27-08-19 à 20:24

Citation :
tu fais intervenir le milieu de [CD] avec la relation de Chasles.

Doit I le centre de [CD].
Je l'introduit dans MC ou MD?

Posté par
lakere : Géométrie : similitude directe et suite de points 27-08-19 à 20:44

Encore une fois désolé. L'erreur est humaine...

Citation :
Je l'introduis dans MC ou MD?


Les deux et tu développes.

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 27-08-19 à 22:13

(\vec{MI}+\vec{IC}).(\vec{MI}+\vec{ID})=nombre
Or \vec{IC}=-\vec{ID}
Et après je cale

Posté par
lakere : Géométrie : similitude directe et suite de points 27-08-19 à 23:29

(\vec{MI}+\vec{IC}).(\vec{MI}+\vec{ID})=\vec{MI}^2+\vec{MI}.\underbrace{(\vec{IC}+\vec{ID})}_{\vec{0}}+\underbrace{\vec{IC}.\vec{ID}}_{-\dfrac{\vec{CD}^2}{4}}

(\vec{MI}+\vec{IC}).(\vec{MI}+\vec{ID})=MI^2-\dfrac{CD^2}{4}

Si bien que:

\vec{MC}.\vec{MD}=k\iff IM^2=k+\dfrac{CD^2}{4}

Pour que les points M existent, il faut que le dernier membre soit positif ou nul.
Tout dépend de la valeur de k...

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 28-08-19 à 20:29

C'est compris, passons à ces suites de points maintenant
4)a) on a S a pour angle /2 or An+1=S(An) donc (IAn;IAn+1) = /2 donc IAnAn+1 est rectangle en I.

Posté par
lakere : Géométrie : similitude directe et suite de points 28-08-19 à 20:45

En fait, 23h19 est la démonstration du théorème de la médiane:

Tu pourras regarder si tu veux.

Oui pour 4)a)

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 28-08-19 à 20:49

Merci

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 28-08-19 à 21:04

Pour démontrer que l'angle ((AnI;An+1I)=π/6+2kπ comment faire ?

Posté par
lakere : Géométrie : similitude directe et suite de points 28-08-19 à 21:23

(\vec{IA_n},\vec{IA_{n+1}})=-\dfrac{\pi}{2}\;\;[2\pi]

Le triangle IA_nA_{n+1} est donc rectangle indirect et la mesure principale de (\vec{A_nI},\vec{A_nA_{n+1}}) est comprise entre 0 et \dfrac{\pi}{2} (n'hésite pas à faire un dessin). (\vec{A_nI},\vec{A_nA_{n+1}})=\widehat{A_n} +2k\pi   (l'angle géométrique \widehat{A_n})

De plus I_A_{n+1}=\dfrac{\sqrt{3}}{3}IA_n (le rapport de la similitude S)

   Donc en parlant d'angles géométriques, \tan\,\widehat{A_n}=\dfrac{IA_{n+1}}{IA_n}=\dfrac{\sqrt{3}}{3} et \widehat{A_n}=\dfrac{\pi}{6}

  Du coup,  (\vec{A_nI},\vec{A_nA_{n+1}})=\dfrac{\pi}{6}+2k\pi

Tout ceci est un peu filandreux mais j'ai voulu éviter les angles orientés...

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 28-08-19 à 21:29

Je croyais que c'était π/2 l'angle de S et non -π/2

Posté par
lakere : Géométrie : similitude directe et suite de points 28-08-19 à 21:41

Ah non:

  Un rapport de similitude est positif par définition.

  S=r'\circ h

r' est une rotation d'angle \dfrac{\pi}{2} donc une similitude directe de rapport 1 et d'angle \dfrac{\pi}{2}

h est une homothétie de rapport négatif donc une similitude directe de rapport +\dfrac{\sqrt{3}}{3} et d'angle \pi

S est donc une similitude directe de rapport +\dfrac{\sqrt{3}}{3} (le produit des rapports) et d'angle \dfrac{\pi}{2}+\pi\equiv -\dfrac{\pi}{2}\,\,[2\pi] (la somme des angles).

A retenir: Une homothétie de rapport k<0 est une similitude directe de rapport -k>0 et d'angle \pi

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 28-08-19 à 21:53

Bien reçu.

Posté par
lakere : Géométrie : similitude directe et suite de points 28-08-19 à 21:59

Je pense qu'il est grand temps de poster un dessin...

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 29-08-19 à 16:03

Voilà d'abord la figure des deux ensembles

Géométrie : similitude directe et suite de points

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 29-08-19 à 16:04

Maintenant comment placer I centre de S ?

Posté par
lakere : Géométrie : similitude directe et suite de points 29-08-19 à 16:08

Si tu as bien travaillé, tu sais en principe qu'il est inclus dans l'ensemble \Gamma_1\cap\Gamma_2

Cet ensemble ne comporte que deux points.

Il s'agit de choisir le bon!

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 29-08-19 à 16:12

I appartient à1 car (IC,ID)=-π/2
Maintenant comment monter qu'il appartient aussi à2?

Posté par
lakere : Géométrie : similitude directe et suite de points 29-08-19 à 16:18

S est une similitude de rapport \dfrac{\sqrt{3}}{3} et S(C)=D

Donc ID=\dfrac{\sqrt{3}}{3}\,IC et ID^2=\dfrac{1}{3}\,IC^2

Autrement dit 3\,ID^2-IC^2=0

Vois-tu le lien avec \Gamma_2 maintenant ?

Posté par
lakere : Géométrie : similitude directe et suite de points 29-08-19 à 16:25

D'ailleurs c'est plutôt \Gamma_1 ...

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 29-08-19 à 16:34

Ah,bon merci.

Posté par
lakere : Géométrie : similitude directe et suite de points 29-08-19 à 16:36

Alors ce point I: celui du haut ou celui du bas ?

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 29-08-19 à 16:38

Du haut

Posté par
lakere : Géométrie : similitude directe et suite de points 29-08-19 à 16:40

Yesss!

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 29-08-19 à 18:17

4)b) voilà les points

Géométrie : similitude directe et suite de points

Posté par
mathafou Moderateurre : Géométrie : similitude directe et suite de points 29-08-19 à 18:31

Bonjour,

il serait sans doute profitable de faire figurer les droites/segments AnAn+1
- vu qu'on en parle implicitement dans l'énoncé (en vecteurs)
- vu que c'est la méthode la plus expéditive et efficace de construire de façon précise et pas au pifomètre à main levée les points An eux même...

Posté par
lakere : Géométrie : similitude directe et suite de points 29-08-19 à 20:04

Ça ressemble à ce que j'avais obtenu:

  Géométrie : similitude directe et suite de points

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 30-08-19 à 20:46

4)a) on a
a_0=\frac{1}{2}(IC)(ID)
Avec IC=\frac{\sqrt{3}}{3}IC
Donc\frac{\sqrt{3}}{6}IC²
Or, IC=CD cos(/6)=3*3/2=3/2
Donc IC²=9/4

Ainsi, a0= \frac{\sqrt{3}\times9}{6\times4}=\frac{3\sqrt{3}}{8}

_Oui, je pense aussi que ça devrait être\frac{\sqrt{3}}{6}\times(IA_n)²
défaut du sujet

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 30-08-19 à 20:57

4)d) (an) est une SG de raison 1/3
\lim_{+infini}(a_0+a_1+...+a_n)=\lim_{+infini}(a_0\frac{1-(\frac{1}{3})^{n+1}}{1-(1/3)}=\frac{3a_0}{2}=\frac{9\sqrt3}{16}

Posté par
lakere : Géométrie : similitude directe et suite de points 30-08-19 à 22:09

Très bien

Posté par Profil Fifaliana36re : Géométrie : similitude directe et suite de points 31-08-19 à 17:51

Merci

1 2 +


Rechercher
Menu
Espace membre
6 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1730 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !