Bonjour, je suis en seconde et pour jeudi j'ai un Dm de maths et il me reste un exercice que je ne comprends pas du tout. J'espère que vous pourrez m'aider.

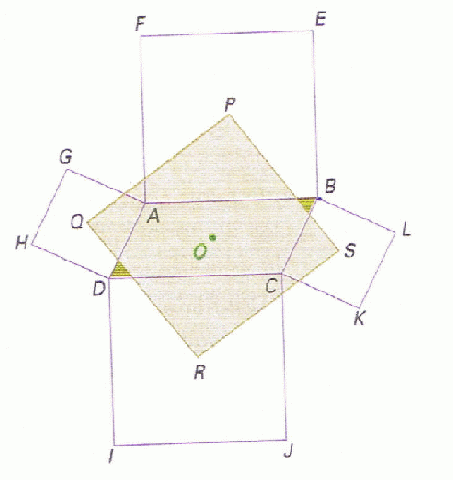
Intro : Le but de cet exercie est de démontrer que le quadrilatère PQRS est un carré, la figure étant constituée de 4 carrés construits extérieurement au parallélogramme ABCD :
Shéma (en bas)

1. On considère la symétrie de centre O.
a) Quelles sont les images des points A et B. Je l'ai fait
b) Justifier que l'image du point E est le point I.
c) En déduire que l'image du point P est le point R.
d) Que peut on déduire de la nature du quadrilatère PQRS ?

2. On note "m" la mesure de l'angle BPS
a)Montrer que les triangles PBS et PAQ ont en commun les longueurs de 2 cotés adjacents à un angle de même mesure.
On admet alors que ces deux ttriangles sont superposables.
b) Que peut on alors en déduire a propos de la mesure des angles BPS et APQ, et de la longueur des cotés PQ et PS.
c) En déduire que le quadrilatère PQRS est un losange.
d) Montrer que l'angle QPS = 90°
e) Conclure sur la nature du quadrilatère PQRS.

S'il vous plait aidez moi ! merci !