décomposer ce vecteur suivant les trois droites

Que signifie décomposer ce vecteur suivant les trois droites ?

En éffet, AB est en qlq sorte la resultante des projection sur les axes.

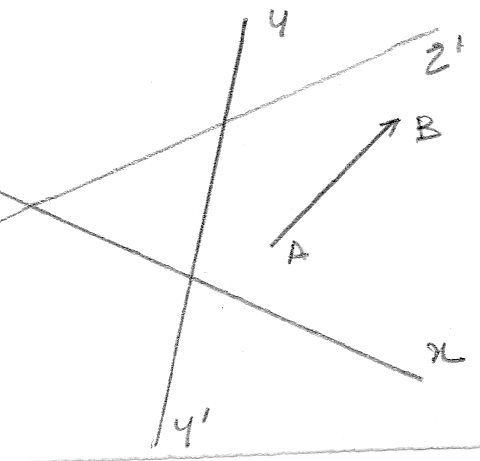
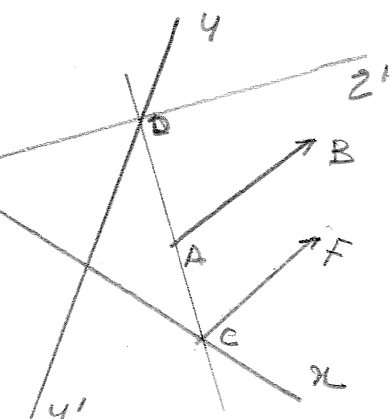
il se peut qu'on soit obligé tout d'abord de faire glisser le vecteur AB sur l'axe x'x  par un vecteur équipollent CF dont l'extrémitéest sur l'axe x'x. A partir de C, on tracela droite CD, avec D,le point de rencontre des axes y'y et z'z.

c'est tout ce que j'ai pu avoir  comme explication.

Bonjour
tu peux donner ton énoncé complet, au mot près ?
et si tu as un cours où on définit l'expression "décomposer un vecteur du plan selon trois droites", nous recopier cette définition ?

l'énoncé est tel que je vous  ais  fait  parvenir, et rien d'autre.
merci.

tu as bien eu un cours, avant ?

Bonjour

A mon avis, les droites ne sont pas dans un plan mais dans l'espace!

Bonjour camélia
c'est pour ça que je lui demandais de recopier son énoncé au pot près .... mais Crystalle a l'air formel(le) ...

Salut lafol

au pot près

Si l'énoncé est juste... il est faux!

gloops ! j'ai visé trop haut sur mon clavier !

Bonjour à tou(te)s,

Désolé de déterrer ce vieux sujet mais je suis confronté au même exercice et ne trouve pas de solution, j'aurais tendance à projetter orthogonalement le vecteur sur les trois axes mais mais pour quel résultat ??

Quid du dernier post de crystalle sur les intersections des axes ?? Si quelqu'un peut me mettre sur la voie je vous en serais très reconnaissant.

Au fait, l'énoncé complet (en tous cas pour ma part) :

"Dans un plan P on donne trois droites quelconques : x'x  y'y  z'z et un vecteur AB

1 - Décomposer ce vecteur suivant les trois droites.
2 - Montrer que la décomposition n'est possible que d'une seule manière

D'après Camélia : "les droites ne sont pas dans un plan mais dans l'espace", pourtant l'énoncé spécifie bien un plan P pour les trois droites...

Merci

il y a une erreur dans l'énoncé, il n'y aura jamais unicité de la décomposition d'un vecteur dans une famille qui n'est pas libre

D'accord!

par curiosité, il sort de où ce texte ? ça a l'air aussi mal fichu que l'autre vu hier sur les trièdres?

je pense à ça : problème sur les trièdres

Bonjour et merci de vos réponses,

L'énoncé est peut-être mal formulé (en tous cas, pour le coup, il est mot pour mot et accompagné du shéma ci-joint sans les traits rouges) ??
Peut-être qu'il existe un plan P mais que les 3 droites ne s'y trouvent pas toutes ??

Sinon, c'est peut-être justement la réponse au 2)(Montrer que la décomposition n'est possible que d'une seule manière ) -> pour que ce soit possible il faut que les trois axes ne se situent pas dans le même plan ??

En tous cas AB est n'est pas du tout la résultante des projections sur les axes SI ces axes sont dans le même plan (voir image jointe)...


En tous cas merci de votre aide

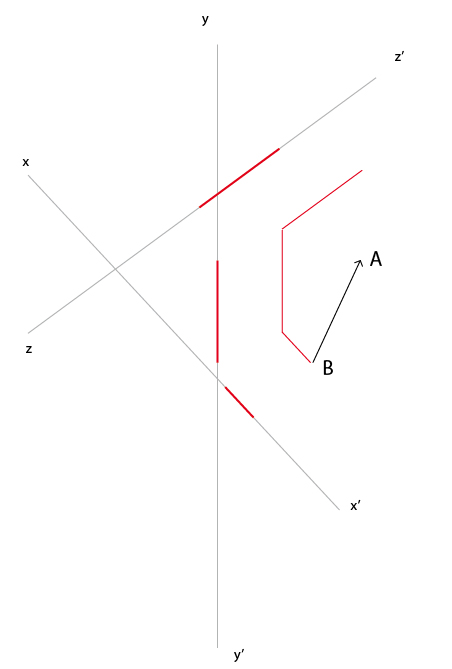
Bonjour ugolin83

"trois droites quelconques : x'x  y'y  z'z"
alors prenons un contre exemple:
je choisi x'x à et y'y confondu avec z'z"

je décompose comme la somme de sur x'x et de la somme de 2 vecteurs opposés sur y'y et z'z"
la décomposition n'est pas unique !

mais

> Chatof Bienvenue au club!