Inscription / Connexion Nouveau Sujet
Hélicoide cylindrique.
Bonjour à tous,
Existe t'il un tracé pour développer géométriquement cette hélicoïde cylindrique?
Cordialement
Bonjour,
Ça dépend.
Si tu parles d' hélicoïde cylindrique, cela signifie que la surface est engendrée par une droite variable (on dit une surface réglée) s' appuyant sur une hélice cylindrique.
Toute la question est de savoir avec précision comment est définie cette droite; par exemple:
-Hélicoïde aigu (ou gauche): la droite s' appuie sur une l'hélice cylindrique et sur l' axe du cylindre sur lequel elle est tracée en formant avec cet axe un angle aigu constant.
-Hélicoïde normal: la droite est perpendiculaire à l' axe.
-La droite reste constamment tangente à l' hélice.
ou autres....
Et bien sûr, ton dessin ne permet de savoir à qui on a affaire...

Bonjour Lake et merci pour ces précisions. Le mieux c'est que je demande directement à mon fournisseur. Tout ce que je peux dire c'est que le pas et égal à la hauteur du cylindre...
De ce que je vois sur ton dessin (mais ça reste une supposition), je pencherais pour un hélicoïde normal.
C' est à dire engendré par une droite s' appuyant sur l' hélice et l' axe du cylindre en restant perpendiculaire à cet axe.
Mauvaise nouvelle: il n' est pas développable...

Bonsoir Lake et merci pour ta réponse.
Donc,si admettons si c'est ce genre d'hélicoïde, dite normale et qu'elle n'est pas développable, comment font ils en tôlerie par exemple, pour découper la tôle sans patron d'après toi?
Je ne connais qu' un (petit) côté mathématique de la chose. Il faudrait poser la question à un chaudronnier.
En procédant artisanalement, je suppose qu' on utilise un développement "approché" (je ne sais pas faire). Je pense que dans l' industrie, les machines numériques savent faire...
Autre chose:
-Hélicoïde aigu (ou gauche): la droite s' appuie sur une l'hélice cylindrique et sur l' axe du cylindre sur lequel elle est tracée en formant avec cet axe un angle aigu constant.
-Hélicoïde normal: la droite est perpendiculaire à l' axe.
-La droite reste constamment tangente à l' hélice.
Pour ne pas t' influencer, je n' ai pas donné le nom du dernier:
C' est "l' hélicoïde développable"
Et c' est le seul

Bonsoir Lake et merci!
Oui je crois qu'ils envoient les fichiers des développés vers une machine FAO (fabrication assistée par ordinateur)...Pour ma part j'utilise le logiciel pour loisirs, à la limite imprimer en 3d,c'est tout. Mon premier métier était peintre en bâtiment. J'ai fais un peu de descriptive en 2005,à l'ief-ctf de Mouchard dans le jura, ça me plaisait et c'est pour cela que je m'y intéresse plus ou moins encore maintenant.
Bon, à quoi ressemble cette hélicoïde développable?
J' aime beaucoup la descriptive aussi 
Bon, à quoi ressemble cette hélicoïde développable?
C' est un peu ce que je craignais

Je vais avoir pas de boulot avec GeoGebra mais plus ce soir; ça me prend beaucoup de temps...

D' abord une perspective qui montre comment est construit un hélicoïde développable.
Une hélice circulaire de pas sur un cylindre de diamètre
La tangente en à l' hélice engendre l' hélicoïde développable lorsque
décrit l' hélice.
A droite sur la figure, le développement de l' hélice (c' est une droite).
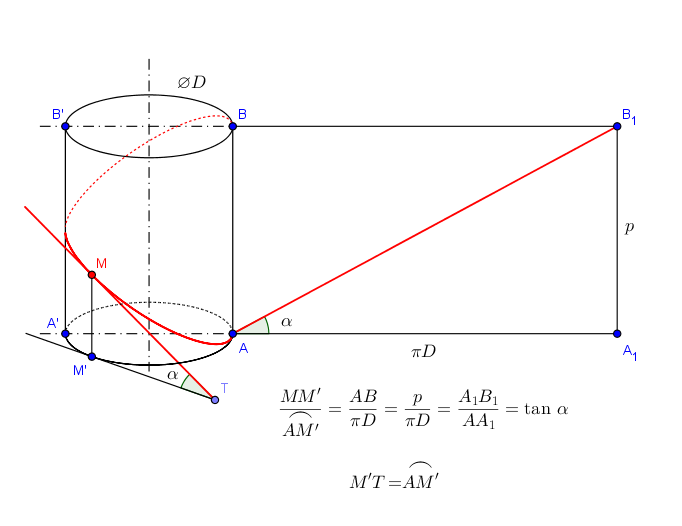
La suite plus tard...

Bonjour Lake et merci!
J'ai trouvé des documents concernant les hélicoïdes mais apparemment, on ne peut pas les poster ici...
Bon sinon, jusqu'à là ,je suis!
En premier lieu, une épure d' un hélicoïde développable:
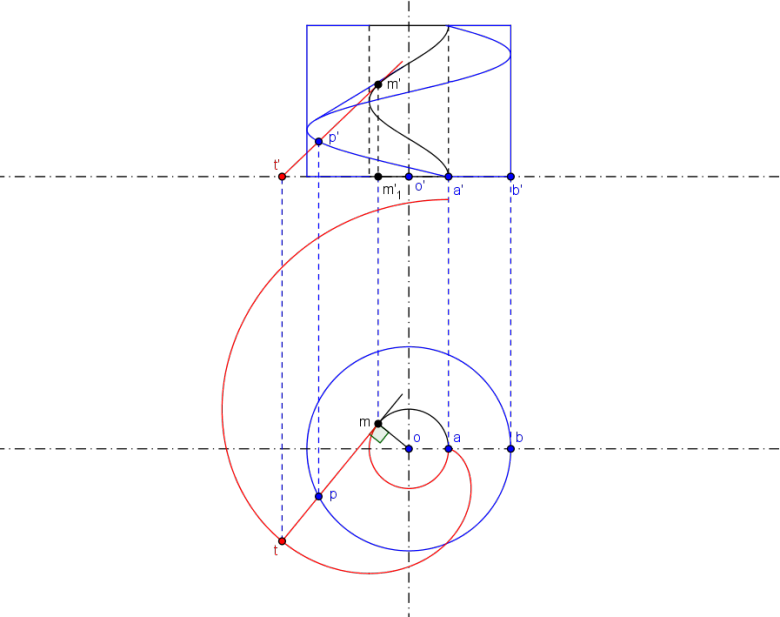
On commence par l' hélice sur le cylindre intérieur (l' hélice directrice):
La cote du point courant est proportionnelle à l' arc
et le coefficient est
(voir la perspective au dessus)
donc on reporte sur la ligne de rappel de la longueur:
pour obtenir le point courant
de l' hélice directrice (en noir).
On construit ensuite la tangente à cette hélice qui recoupe le plan horizontal de projection en
En projection horizontale, cette tangente est tangente en au cercle projection du cylindre de base et
(toujours garder un oeil sur la perspective).
On reporte avec une ligne de rappel.
Lorsque décrit l' hélice directrice, le point
décrit une section horizontale de l' hélicoïde (une développante de cercle: l' espèce de spirale en rouge sur la figure).
Reste à couper l' hélicoïde par un cylindre extérieur pour le visualiser (en bleu); on obtient une seconde hélice de point courant et de même pas que l' hélice directrice (en bleu).
Le développement plus tard...

Bonjour Lake et merci
Je voudrais déjà quelques explications concernant l'épure de l'hélicoïde développable et surtout voir ce que l'hélicoïde terminée représente sur la perspective.
L'hélice bleu et noir sont de même pas?
Cordialement
L' hélice noire sur l' épure correspond à celle de la perspective. C' est l' hélice "directrice" de l' hélicoïde. Sur cette perspective, l' hélicoïde n' est pas représenté.
La tangente engendre l' hélicoïde lorsque
décrit cette hélice. La surface est alors illimitée vers l' extérieur du cylindre de base.
Pour la limiter, on la coupe par un second cylindre de même axe et de diamètre supérieur au cylindre de base. L' intersection cylindre/hélicoïde est une seconde hélice de même pas que l' hélice directrice en bleu sur l' épure.
Il faut bien se rendre compte qu' en projection frontale, une partie de l' hélicoïde sectionné par le plan horizontal de projection se trouve projetée sur un segment qui va de à un point entre
et
(pas représenté sur l' épure)
Ce segment correspond à la partie de la développante de cercle rouge (la spirale) comprise entre les deux cylindres en projection horizontale. C' est la trace de la tangente sur le plan horizontal de projection.
Dès que la tangente est assez "haute", elle coupe le cylindre extérieur avant de couper le plan horizontal de projection et sa trace sur ce cylindre est la seconde hélice (bleue) de même pas que l' hélice directrice.
Deux règles qui peuvent faciliter la compréhension de l' épure:
1) La section d' un hélicoïde développable par un plan perpendiculaire à l' axe est une développante de cercle (la "spirale")
2) La section d' un hélicoïde développable par un cylindre concentrique est une hélice de même pas que l' hélice directrice.
Bon, tout ça n' est pas facile à visualiser. Je ne sais pas si mon baratin est très clair...
Le développement suit; il va falloir admettre certaines choses...

Oui,je comprends mieux, cependant comment retrouve tu la distance qui sépare les points t et p?
Je pense que mon logiciel par défaut génère au autre hélicoïde ,un peu comme si on extrudait la largeur l'hélice directrice pour obtenir l'hélicoïde.
Le développement:
L' hélice directrice sur une spire a une longueur (voir la perspective)
On pourrait la développer sur une circonférence de rayon
Mais, et c' est là que je te demande d' admettre certaines choses, le développement de l' hélicoïde nécessite de la développer sur une circonférence plus grande de rayon :
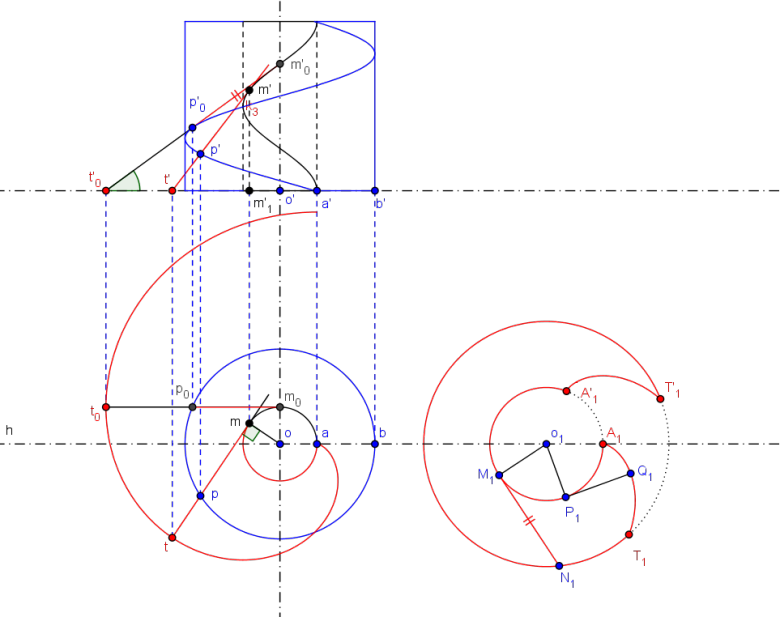
La longueur de la spire d' hélice directrice est l'arc
La vraie grandeur d' une génératrice est vue en projection frontale en ; les génératrice se développent suivant les tangentes au cercle
. Une de ces génératrices est reportée en
La courbe transformée de la seconde hélice dans le développement est aussi une circonférence de centre
Les arcs de développante de cercle se transforment en d' autres arc de développante du cercle Par exemple:
Peut-être un peu indigeste ? 

la distance entre le point t et p en vue de dessus?
Regarde la perspective:
Si bien qu' en projection horizontale:

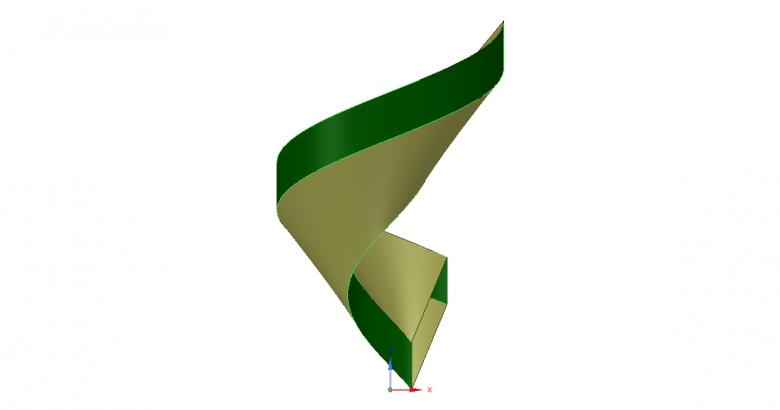
J'ai modélisé ton hélicoïde enfin de pense, avec mon logiciel, donc en jaune orangé ça serait l'hélice directrice,l'autre hélice et sur le cylindre transparent (même axe pour les 2 cylindres).
La hauteur et le pas de 2 hélices sont identiques, ça correspondrait ?
A vue de nez, je pense que tu as modélisé un hélicoïde normal, c' est à dire avec des génératrices qui coupent l' axe à angle droit. Le même d' ailleurs que celui avec lequel tu as commencé ce topic.
Pour l' hélicoïde développable, les génératrices sont tangentes à l' hélice directrice.

Bonjour et merci,
Donc,ça serait une hélicoïde génératrice tangente?un peu comme si on extrudait verticalement l'hélice directrice?Dans ce cas la feuille de métal ne subit aucune déformations?
Non, non: tes surfaces (de ce que je vois il y en a deux) sont engendrées par une droite parallèle à l' axe et s' appuyant sur une hélice. En ce sens, ce sont bien des hélicoïdes (en fait ce sont des cylindres!) mais pas des hélicoïdes développables.
Je te propose deux choses pour visualiser une perspective:
1) Aller faire un tour sur le site "mathcurve" (une mine pour les courbes et surfaces) de Robert Ferréol ici: ![]() (clique sur la maison)
(clique sur la maison)
2) Si tu as les moyens techniques de faire:
Réaliser un patron du développement de 12h28 (je sais, il n' y a pas de cotes mais un patron approximatif suffit) dans une matière "souple": mince feuille de métal voire une feuille de papier. Tu oublies les génératrices représentées en et
et tu ne tiens compte que des arcs de cercle limités par les arcs
et
. Bref, tu réalises une surface plane comprise entre les deux cercles (donc évidée au milieu) et limitée par les deux arcs précédents.
Une fois réalisé, tu t' arranges pour que les deux points et
restent sur le plan de ton établi/table et tu "tires" sur le point
en sorte de l' amener à la verticale du point
un peu plus haut. La distance verticale
représentera le pas de l' hélice directrice.
En principe, si tout se passe bien, la surface de ton patron se voilera et représentera l' hélicoïde développable. Normalement, tu dois déformer ton patron de manière à ce que les points et
restent sur le plan de l' établi/table et que les points
et
soient dans un plan parallèle à ton établi/table "au dessus" avec les points
1 et
sur une même verticale.
Si tu suis cette voie, j' espère que tu nous donneras tes impressions...
Une dernière chose:
Mon premier métier était peintre en bâtiment.
Se mettre à la descriptive sur le tard: pas ordinaire! Tu as toute ma sympathie...
Confidence pour confidence, je suis un ancien mineur de fond (au charbon).
Je pense qu' on sait tous les deux ce que travail veux dire...

Bonjour Lake et merci.
Oui, j'avais appris quelques bases, parce que je voulais me perfectionner en plâtrerie traditionnelle, depuis je ne pratique plus ces métiers. Pour le métier de peintre, c'est différent, le fait d'habiller des surfaces planes, par exemple, ne demande pas spécialement d'avoir des notions de descriptives enfin voilà.
.
Bon, dans ce cas comme je n'arrive pas à visualiser la géométrie ( l'hélicoïdes développable),c'est une très bonne idée!J'ai le développement de l'hélicoïde...
Juste une précision, lorsque tu déformeras ton patron en amenant au dessus et à la verticale de
, l' arc complet
doit rester sur le plan de ton établi/table mais à partir de cet arc, le patron se voilera en principe vers le "bas". Et l' arc complet
doit être dans un plan horizontal parallèle à ton établi/table et "au dessus".
Je suis curieux et intéressé: si tu réalises un patron, fais nous part des résultats de ton "expérience"

Oui, tout est à la même échelle mais voici un patron coté qui convient pour un pas de 9 et un rayon de 1.95 pour le cylindre support de l'hélice directrice:
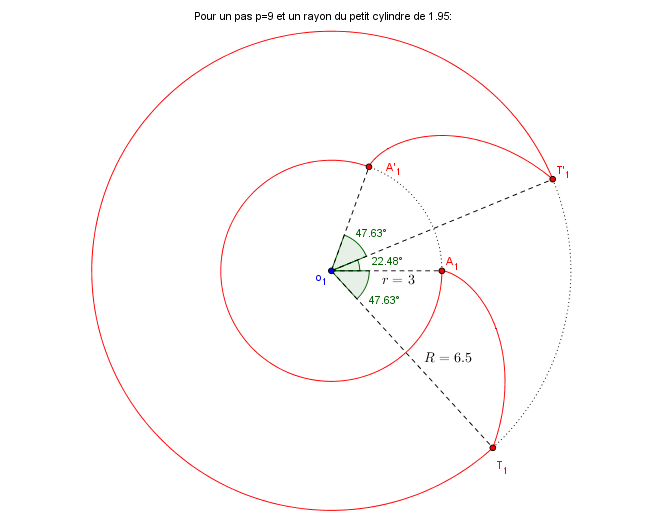
L' idéal étant d' enrouler le patron sur un cylindre de 1.95 de rayon et de 9 de haut.
Mais pourquoi est elle développable?
Je ne peux pas te répondre simplement; grossièrement, la déformation quand tu aplatis l' hélicoïde pour obtenir le patron est exactement compensée par l' agrandissement du diamètre central. Si tu réalises un patron, tu verras mieux ce qui se passe quand tu le déformeras pour obtenir l' hélicoïde.

Bon, je pense que j'ai "enfin" compris la méthode de construction de cette fameuse hélicoide,le fait de définir sur le cylindre un système réguliers de génératrice permet de pouvoir tracés les tangentes à ses cercles (base et sommet).Enfin,je préfère que tu jette un il sur le fichier.
Merci! Donc après tu recoupes l'hélicoïde avec un autre cylindre "plus grand",oui, pourquoi pas! Bon maintenant je n'ai plus qu'à reproduire l'épure.
@+!
Donc après tu recoupes l'hélicoïde avec un autre cylindre "plus grand"
Exactement, dans le but de limiter la surface et de voir l' intersection de ce second cylindre et l' hélicoïde qui donne une seconde hélice de même pas que la première.

Bonjour Lake,
Donc voilà, la génératrice en bleu clair serait en vg en projection frontale.
Bon,je te laisse regarder.
Bonne journée!
Bonsoir,
Ça ne vas pas: les génératrices sont tangentes à l' hélice directrice et en projection elles doivent être tangentes aux projections de l' hélice. Sur ton épure, en projection horizontale, les génératrices projetées sont bien tangentes au cercle projection de l' hélice directrice mais en projection frontale, les génératrices projetées ne sont pas tangentes à la projection de l' hélice directrice.
Regarde l' épure de 15h49:
est tangente au cercle projection horizontale de l' hélice directrice et
est tangente à la projection frontale (en noir) de l' hélice directrice.
Tu dois avoir un problème dans ta construction...

Bonjour Lake,
Oui...je viens de me rendre compte sur ma modélisation 3 D que les génératrices ne sont pas tangentes à l'hélice directrice.
Donc, les génératrices tangentes à l'hélice directrice sont toutes de même pentes, donc en projection horizontale,en les recoupant sur un plan parallèle à la base du cylindre on obtient cette spirale, reste à la recouper l'hélicoïde avec un deuxième cylindre d'un diamètre supérieur.
*Avec mon logiciel, je joins 11 génératrices sur 12... (pour créer la surface) pas moyen de modéliser entièrement cette hélicoïde...
Bon,honnêttement je ne sais pas si je peux reproduire l'épure.
Déjà,je ne sais pas tracer une tangente une l'hélice , ensuite, bon même si j'en ai une en vg,comme la rouge sur mon dernier fichier posté, comment faire pour les 11 autres, et comment les projeté sur les deux projections (verticale/horizontale) pour définir la deuxième hélice?
Bon sinon j'abandonne.
Commence par oublier les perspectives dans un premier temps. On se limite à une épure comportant une projection horizontale et une projection frontale.
Tout ce que je vais écrire se rapporte à l' épure de 15h49.
Une remarque: l' hélice directrice a un pas "à gauche". Les tiennes ont un pas "à droite" mais peu importe.
On commence par l' épure de l' hélice directrice de pas sur le cylindre de diamètre
de point courant
Par projection horizontale d' un point courant de l' hélice (donc sur le cercle projection du cylindre), on mène une ligne de rappel qui recoupe la ligne de terre en
A partir de , on reporte verticalement en projection frontale, la longueur
où
est la longueur de l' arc
en rouge sur l' épure.
On obtient ainsi la projection frontale du point courant de l' hélice directrice.
Il suffit de répéter l' opération pour plusieurs points pour obtenir l' hélice directrice en noir point par points
La tangente à l' hélice directrice:
En projection horizontale, on mène par la perpendiculaire à
Sur cette perpendiculaire, on reporte la longueur (toujours la même longueur d'arc) à partir de
pour obtenir la trace
de la tangente sur le plan horizontal de projection.
On obtient la projection frontale sur la ligne de terre par une ligne de rappel.
On obtient ainsi les projections horizontale et frontale de la tangente en et
Il suffit de répéter l' opération pour plusieurs points pour obtenir autant de tangentes que l'on veut et donc l' hélicoïde "droite par droite"
Il est ensuite facile d' obtenir l' intersection de ces tangentes avec un second cylindre en

Oui,je comprends que tu détermines des points sur la projection horizontale et que tu les projettes en projection frontale sur l'hélice directrice, mais ma question est de savoir comment procèdes-tu pour que les génératrices soient tangentes à l'hélice directrice (exemple: m 't' ) afin qu'elle soit projetée "au bon endroit sur la ligne de terre?. image du 20/4 à 12h28.J'ai vu une méthode sur un site.
Donc c'est Homeomath (construire une tangente à la courbe d'une fonction )
*pour la construction de la spirale,j'ai compris.
Par construction, la droite est tangente à l' hélice directrice.
Si tu suis pas à pas les indications de 16h34, la droite sera automatiquement tangente à l' hélice directrice au point

je reporte la distance (a,m) sur la ligne de terre à partir m'1 et donc j'obtiens t'.
Ensuite, je projette t' sur la projection horizontale et l'intersection avec la tangente (mp) nous donne le point t de la spirale.
Si tu fais n' importe quoi, c' est sûr que ça ne marchera pas.
Je t' ai indiqué la marche à suivre à 16h34. C' est toi qui vois.
Bonsoir Lake et meilleurs vux. J'ai redessiné la figure, je te laisse regarder.
Meilleures salutations.

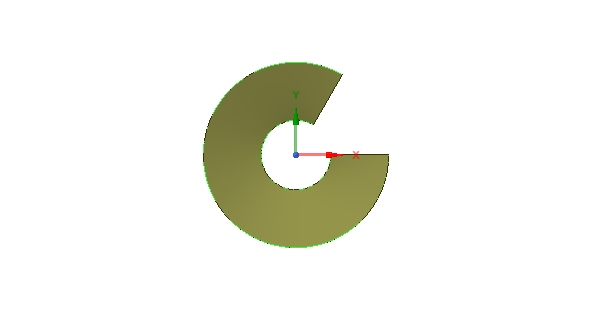


 géométrie en Bts
géométrie en Bts