Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Géometrie plane et dans l'espaceTopics traitant de Géometrie plane et dans l'espace [tout]Lister tous les topics de mathématiques
Niveau terminale
Inclusion des images par f
Posté par sgu35
Bonjour, j'ai une question qui peut paraître triviale mais je n'arrive pas à la démontrer :
soit f une fonction quelconque,
si , alors
.
bonsoir
il suffit de l'écrire !
pour montrer qu'un ensemble est inclus dans un autre, on prend un élément de celui de gauche et on démontre qu'il est dans celui de droite 
voilà
je préciserais juste :
sgu35 @ 06-07-2021 à 18:49
J'ai trouvé la solution :
Soit)
il existe un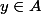 tel que
tel que 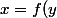)
or,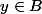 car A
car A  B
B
donc\in f(B))
donc)
d'où\subset f(B))
J'ai trouvé la solution :
Soit
il existe un
or,
 B
B
donc
donc
d'où
sgu35 @ 06-07-2021 à 18:50
D'accord
Autrement, je voudrais savoir d'où vient le fait que si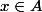 ,
, \in f(A))
D'accord
Autrement, je voudrais savoir d'où vient le fait que si
c'est quoi la définition de l'image par f d'un ensemble A ??????


