Annuler
connectez vous
trigonométrie en post-bac
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Ensemble et application Partie II
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup TrigonométrieTopics traitant de trigonométrie [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Incompréhension TRIGO
Posté par lucie38
Bonjour, je suis en L1 et j'ai un dm à rendre mais je n'ai pas compris quelque chose.
On me demande de démontrer que :
cos(a-b).cos(a+b)= cos²a - sin²b = cos²b - sin²a
Pour ça j'ai réussi et compris grâce à cette démonstration proposé sur ce même forum.
cos(a-b).cos(a+b)= (cosa.cosb + sina.sinb)(cosa.cosb - sina.sinb)
cos(a-b).cos(a+b)= cos²a.cos²b - sin²a.sin²b
cos(a-b).cos(a+b)= cos²a.(1 - sin²b) - (1-cos²a).sin²b
cos(a-b).cos(a+b)= (cos²a - cos²a.sin²b) - (sin²b - cos²a.sin²b)
cos(a-b).cos(a+b)= cos²a - cos²a.sin²b - sin²b + cos²a.sin²b
cos(a-b).cos(a+b)= cos²a - sin²b
Cependant, je n'ai pas compris comment on passe de la première ligne à la deuxième. J'ai essayé grâce à la distributivité.
Mais après avoir simplifié (factorisé) je me retrouve avec ça:
(cosa.cosb)² + (sina - sinb)² - 2(cosa.sina) + 2(cosa.sinb) - 2(cosb.sina) + 2(cosb.sinb)
En espérant avoir été claire,
Merci de votre aide ! 
)
Lucie
Bonjour,
ton interrogation porte sur comment passer de
Citation :
cos(a-b).cos(a+b)= (cosa.cosb + sina.sinb)(cosa.cosb - sina.sinb)
cos(a-b).cos(a+b)= (cosa.cosb + sina.sinb)(cosa.cosb - sina.sinb)
à
Citation :
cos(a-b).cos(a+b)= cos²a.cos²b - sin²a.sin²b
cos(a-b).cos(a+b)= cos²a.cos²b - sin²a.sin²b
ou alors j'ai mal compris
je pense que ce que vous dites est vrai mais je n'arrive pas à le démontrer,
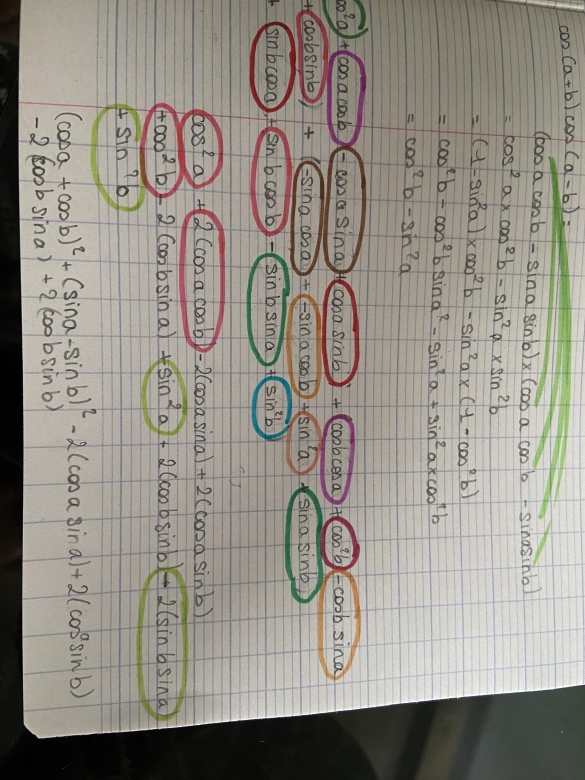
sur la photo, ce qu'il y a en couleur c'est le développement,
en dessous j'ai essayé de regrouper les termes,
pour enfin factoriser,
j'ai sûrement fait une erreur mais je ne la vois pas …
En tout cas merci de votre temps !
tu te trompes quand tu développes : par exemple
il n'est même pas nécessaire de distribuer; si tu poses
et
, on obtient
ça ne te fait penser à rien?
ah oui ! l'identité remarquable... je ne l'avais même pas reconnu merci beaucoup !
Donc, si j'ai bien compris, mon erreur a été de séparer le cos(a) du cos(b) quand j'ai développé ?
J'aurais dû développé comme ceci ? :
cos(a).cos(b) * cos(a).cos(b) + cos(a).cos(b) * (-sin(a).sin(b)) +
(-sin(a).sin(b)) * cos(a).cos(b) + (-sin(a).sin(b)) * (-sin(a).sin(b))
pour finir sur (cosa.cosb)² - (sina.sinb)²
est-ce bien ça ?
merci !
quelques petites erreurs
je reprends tout en distribuant
mais il est préférable d'utiliser l'identité remarquable