Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale IntégrationTopics traitant de Intégration [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Intégrale d'une fonction

Posté par
IamMe 22-01-20 à 14:10

Bonjour, merci de m'aider pour un exercice. En effet je commence les intégrales...

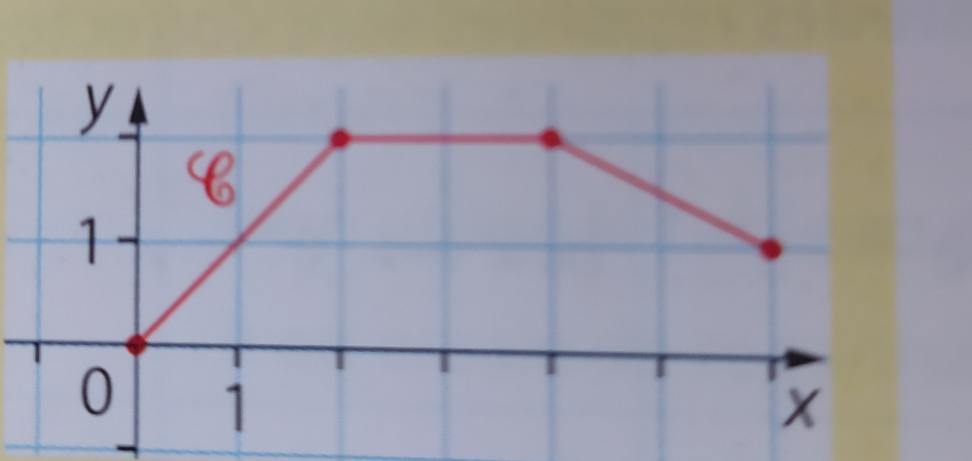
Soit la fonction f définie sur [0;6] par sa courbe représentative C.
Donner toutes les bonnes réponses

1.\int_{0}^{2}{f(x)dx} est égale à :
a.2
b.4
c.\int_{0}^{2}{f(t)dt}

2.\int_{2}^{4}{f(x)dx} est égale à :
a.2
b.4
c.6


3.\int_{0}^{6}{f(x)dx} est égale à :
a.6
b.8
c.9

1. a et c
2.b
3. Je ne vois pas comment la calculer...

La fonction n'est pas donnée, mais seulement sa courbe représentative...

Intégrale d\'une fonction

Posté par
Yzzre : Intégrale d'une fonction 22-01-20 à 14:13

Salut,

Correct pour 1 et 2 ;

Pour la 3 :

\int_{0}^{6}{f(x)dx} = \int_{0}^{2}{f(x)dx} + \int_{2}^{4}{f(x)dx} + \int_{4}^{6}{f(x)dx}

Posté par
IamMere : Intégrale d'une fonction 22-01-20 à 15:51

Je ne vois pas comment calculer la dernière intégrale...

Posté par
malou Webmasterre : Intégrale d'une fonction 22-01-20 à 16:15

aire d'un trapèze ou rectangle plus triangle rectangle
...

Posté par
Yzzre : Intégrale d'une fonction 22-01-20 à 18:35

Ou : 2 carreaux + la moitié de 2 carreaux    

Posté par
IamMere : Intégrale d'une fonction 23-01-20 à 07:05

Ah ok, il fallait encore décomposer... bon j'essayerai d'y penser. Merci !

Posté par
Yzzre : Intégrale d'une fonction 23-01-20 à 10:08

De rien    


Rechercher
Menu
Espace membre
10 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1741 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !