Inscription / Connexion Nouveau Sujet
Intégrale d'une fonction continue de signe quelconque.
Bonsoir je suis en terminale ES. J'ai un exercice à faire sur le chapitre d'intégration et je ne comprend pas trop c'est un chapitre que nous avons commencé pendant le confinement donc c'est très compliqué de comprendre le chapitre et pouvoir faire les exercices. Pourriez vous m'aider ?
Voici l'exercice:
Exercice 15.
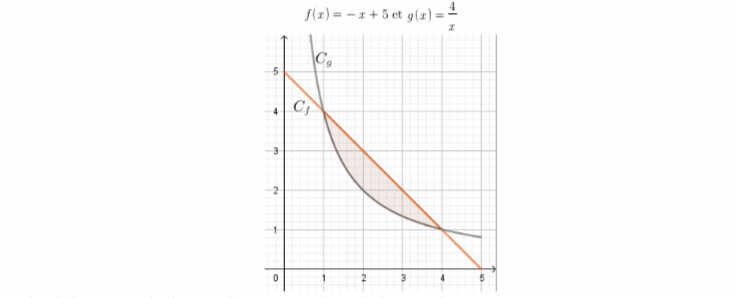
Un responsable marketing réfléchit à la création du logo d'une nouvelle entreprise. Son projet est représenté dans le repère ci- dessous par les courbes Cf et Cg représentatives des fonctions f et g définies sur l'intervalle [0 ; 5] par
f ( x ) = − x + 5 e t g ( x ) = x4
(Il y a une courbe juste ici)
Le but de l'exercice est de déterminer l'aire, en unités d'aire, du domaine coloré. −x2 +5x−4
1. Démontrer que pour tout x∈[1 ; 4], f(x)−g(x)= x . 2. Déterminerlesignede−x2+5x−4surl'intervalle[1;4].
x
3. Déterminer une primitive sur [ 1 ; 4 ] de la fonction x x .
4. En déduire, en unités d'aire, l'aire du domaine coloré.
Je suis désolé je n'avais pas fait attention aux caractères j'espère que c'est compréhensible maintenant.
Un responsable marketing réfléchit à la création du logo d'une nouvelle entreprise. Son projet est représenté dans le repère ci- dessous par les courbes Cf et Cg représentatives des fonctions f et g définies sur l'intervalle [0 ; 5] par
f ( x ) = − x + 5 e t g ( x ) = 4/x
Le but de l'exercice est de déterminer l'aire, en unités d'aire, du domaine coloré.
1. Démontrer que pour tout x∈[1 ; 4], f(x)−g(x)= -x^2+5x-4/x
2. Déterminer le signe de−x^2+5x−4/x sur l'intervalle[1;4].
3. Déterminer une primitive sur [ 1 ; 4 ] de la fonction x=-x^2+5x-4/x
4. En déduire, en unités d'aire, l'aire du domaine coloré.
Bonsoir,
1. Démontrer que pour tout x∈[1 ; 4], f(x)−g(x)= -x^2+5x-4/x
Les parenthèses !!
f(x)−g(x)= (-x^2+5x-4)/x à démontrer...
Car tel que tu l'as écrit c'est plutôt
Ben la question est purement calculatoire... tu as les fonctions f et g qui sont données, il faut juste faire une soustraction...
Oui désolé j'ai oublié les parenthèses.
Pour les 2 premières questions j'ai fait cela:
Pour la première question pour être sûre c'est donc:
On sait que f(x)=-x+5 et g(x)=4/x
On passe alors sur le même dénominateur:
Si f(x)=g(x) alors,
-x+5-4/x= -x*x+5*x/x- 4/x= -x^2+5x-4/x
Ensuite pour la question 2 on utilise delta
Et on trouve 2 racines et le dénominateur et donc supérieur à 0 donc positif. Alors le tableau de signe et donc - et + car a= -1 donc négatif
Je crois que c'est bon ?
Ce qui me pose le plus problème c'est les questions 3 et 4
Oui désolé j'ai oublié les parenthèses.
effectivement !
-x+5-4/x= -x*x+5*x/x- 4/x= -x^2+5x-4/x
et je continue à les oublier !
écrit ainsi c'est totalement faux ton calcul ...
Si f(x)=g(x) alors,
f(x) - g(x) = -x+5-4/x= (-x*x+5*x)/x- 4/x= (-x^2+5x-4)/x
un peu de rigueur s'il te plait
matheuxmatou
Je voulais dire f(x)-g(x)
matheuxmatou
Je n'ai pas fait attention je fais bien plus attention sur mon sujet. Mais sinon le calcul est à faire de cette façon ?
ben oui puisque c'est ce qu'on te demande !
et si tu veux qu'on t'aide et qu'on te corrige tu fais attention partout ... et ici aussi ... 
Si f(x)=g(x) alors,
f(x) - g(x) = -x+5-4/x= (-x*x+5*x)/x- 4/x= (-x^2+5x-4)/x
un peu de rigueur s'il te plait
Je tacherais de plus oublier les parenthèses en vous écrivant.
ben oui puisque c'est ce qu'on te demande !
et si tu veux qu'on t'aide et qu'on te corrige tu fais attention partout ... et ici aussi ...

Oui encore désolé



