Inscription / Connexion Nouveau Sujet
Intégrale multiple
Bonjour,
Je dois calculer l'aire de ce losange avec un changement de variable.
Avec V= X-Y et W = X+Y
D'après le dessin -T/2< X=Y < T/2
Je suis donc la formule de changement de variable et je calcule le jacobien = 1/2 .
Cependant je ne sais pas comment trouver les nouvelles bornes d'intégration en V et W ...
Même chose sur le changement de variable donné ...
Pourriez vous m'expliquer ? Merci bcp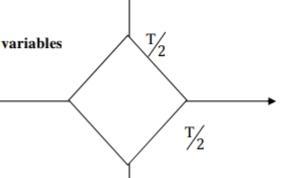
**image recadrée sur la figure** utiliser les moyens mis à disposition pour écrire les maths**![]() [lien]
[lien]
Merci ,
Donc du coup je sais quoi faire mais je reste tjs bloqué avec les bornes de v et w...
Je n'arrive pas à trouver le bon résultat
Tu peux chercher, dans le repère de départ, les équations des droites qui contiennent les côtés du losange ( ici c'est même un carré ).
Par exemple :
quelle est l'équation de la droite passant par les points (0;T/2) et (T/2;0) ?
quelle est l'équation de la droite passant par les points (0;-T/2) et (T/2;0) ?
Donc le changement de variable vient de là, merci
W = T/2 et V = T/2
Je fais donc même chose pour les autres côtés
V= - T/2 et W= -T/2
J'intègre avec V constant (carré de côté T)
Il y a certainement quelque chose de faux...
Donc une s'annule et l'autre pas.
J'ai donc refait le calcul en prenant en compte la valeur absolue.
J'ai donc divisé l'intégrale sur V en deux intégrales (-T/2 ; 0 ) et (0 ; T/2 ).
Car dans le premier intervalle -|v| = v (v négatif)
Et dans le 2eme -|v| = - v (v positif )
J'obtiens donc
T/2 ( [ exp v ] + [ -exp(-v) ] )
Et donc T ( 1 - exp (-T/2 ))
C'est bien cela ?
Je crois que c'est bon, mais je ne suis pas vraiment en forme ce soir et mon avis peut facilement être mauvais.

 1,
1, 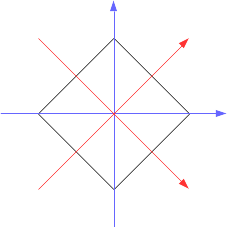


 géométrie en post-bac
géométrie en post-bac