Inscription / Connexion Nouveau Sujet
Intégrales + Tangente
Bonjour, je suis en Terminale S et j'ai un exercice de maths à faire sur les intégrales mais je n'y arrive pas, j'ai un peu de mal avec ce chapitre ^^
Voici l'énoncé :
Soit la fonction F définie pour tout x de l'intervalle [1;+
[ par F(x)=
1/(2t²+7t+3)dt, de représentation graphique C dans un repère orthogonal (O;
;
).
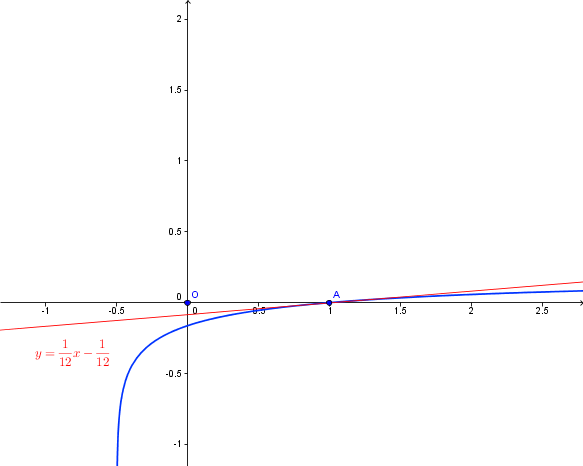
Déterminer une équation de la tangente à la courbe C au point d'abscisse 1.
Je sais que l'équation de la tangente est : y=f'(a)(x-a)+f(a)
Je dois d'abord calculer la primitive de la fonction F non ? Comment faire, parce que la je ne vois pas ^^
Merci d'avance pour votre aide 
Bonjour, désolé je ne comprend pas.. Pourquoi la primitive de la fonction x
1/(2x²+7x+3) est F ?
Enfin, je ne vois pas ce que tu veux dire ^^'
Regarde ton cours:
Soit une fonction continue sur un intervalle
contenant
La fonction définie sur
est la primitive de
qui s' annule en
On a donc et
Annuler
connectez vous