k+1 doit etre au dessus du signe bizarre :§ et k doit etre en dessous de celui ci

Bonjour gratman!

Est-ce que tu as fait un petit dessin? L'idée est de considérer l'aire sous la courbe entre k et k+1, le rectangle "inscrit" dans cette surface et le rectangle "circonscrit" dans cette même surface.

Sur ce topic tu trouves le même raisonnement appliqué à une autre fonction.

Isis

ben enfaite sur le topic je comprend pas grand chose.J ai assister à aucun cour sur ce chapitre donc c pas trés clair.tout sque j ai compris c qu il faut parfois faire l inverse d une dérivée.Enfin voila suis limite la dessus.

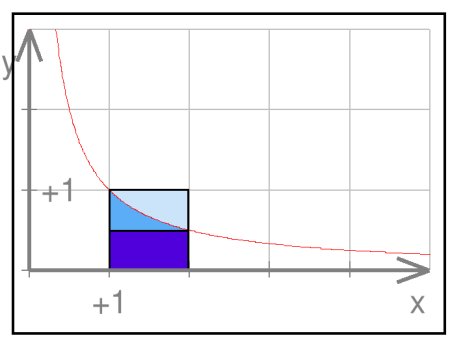
Voilà, avec cette image ça ira peut-être mieux. L'intégrale de k à k+1 est l'aire sous la courbe entre k et k+1. L'idée est de comparer cette aire avec celles des rectangles de ma figure.

Le petit rectangle a une base de 1 (k+1-k) et une hauteur de f(k+1). Son aire est plus petite que l'intégrale.

Le grand rectangle a également une base de 1 et une hauteur de f(k). Son aire est plus grande que l'intégrale.

J'espère t'avoir aidé...

Isis

ok mais comment résoudre mon exercice à l'écrit sans faire de graphique. Je c pas comment je dois m y prendre...

Le graphique est pour l'idée. L'inéquation est immédiate en comprénant l'image. Regarde ton inéquation. elle est bien
et chacun de ces termes correspond à une des aires dont je t'ai parlé.

J'ai pris évidement f(x)=1/x.

Isis

oui je comprend sa maintenant mais pr rédiger sur ma copie je doit faire une courbe montrer l air des retangles et conclure c sa alor ?

>gratman

Soit tu te sens capable de bien expliquer ces notions de rectangles  pour encadrer ton intégrale, soit un petit dessin vaut mieux qu'un grand discours...
Philoux

ok ok merci donc enfaite c est plus simple que sque jle penser jpenser qu il faller utiler des lignes de calcul pr prouver sa.ben c cool merci beaucoup a ceux qui mon aider

>Bon courage

Philoux