- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
interprétation géométrique matrice
Bonjour,
je prépare un concours d'entré pour une école polytechnique. L'algèbre linéaire est un nouveau chapitre pour moi et j'ai quelques difficulté pour ce chapitre.
J'aimerais bien savoir une méthode pour donner une interprétation géométrique d'une application quelconque (voir question 4.2)
Je souhaiterais également de l'aide sur la dernière question: comment calculer (A-B)^n.
Merci de votre aide,
bonne soirée
** image supprimée **
* Océane > glouvincs si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum. *
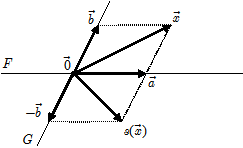
Ici les choses s'arrangent bien. En effet, selon le point 4.1, l'on a que . Ainsi a-t-on que
. Autrement dit, à tout
dans
, il existe
unique dans
tel que
, si bien que
. Il s'agit visiblement de la symétrie [vectorielle] par rapport à
de direction (sic)
.
Précision : Peux-tu calculer ? Puis
?
A +
Salut DHilbert,
merci pour ta réponse. Si on calcule det A on trouve det A = -1
et A² = ( 1 0 )
( 0 1 )
Je suis vraiment novice dans ce chapitre et je ne comprends vraiment pas comment tu as déduit qu'il s'agissait d'une symétrie vectorielle.
Peut on grâce à la question 4.1, se servir de celle-ci pour reconnaitre le type d'application que c'est ? ou grace au déterminant de la matrice application. Je rame vraiment sur ce genre de question et j'ai beaucoup cherché sur internet des explications sur ce sujet mais pas grand chose m'a réellement convaincu. C'est d(autant plus dure quand on n'a pas la chance de suivre des cours sur ce chapitre ! et qu'on doit préparer un exam. C'est niveau bac +1 je pense... Merci d'apporter ton aide!
Lorsque tu sortiras de prison : Pour tout te dire, j'ai calculé de tête (résultat que tu donnes !) et je me suis essentiellement focalisé sur le 4.1 qui donne, en dimension deux, une bonne vision des choses.
Question : Quand passeras-tu ton concours ?
A +
Bonjour,
Tout d'abord, veuillez m'excuser pour l'image. Quelle erreur j'ai fait la, je voulais juste plus de clarté dans l'enoncé. On me dira qu'il existe le code latex ... Voilà je suis désolé. Concernant mon exam, il est en août. Je dois te dire que je comprends pas trop comment tu fais. Je ne vois pas trop le lien avec les déterminants. Mais bon je vais pas vous embêter av des trucs qui semblent plutôt basiques. Je suis venu ici poser la question. Je vous mets au défi de trOuver une page sur internet où l'on explique rigouresement comment faire. Devrais-je plus m'orienter dans les livres?
Très rapidement : Ce qui caractérise une symétrie vectorielle d'un
-espace vectoriel
de dimension finie
, c'est que
. L'on dit encore que
est un automorphisme involutif de
. Par suite, l'on peut écrire que
et l'on dit que
est la symétrie par rapport à
suivant [ou de direction]
. Il faut faire attention sur le fait que les
-sous-espaces vectoriels
et
ne sont pas forcément orthogonaux.
Exercice rapide motivé par ton exo : Soit associée à un endomorphisme
. Caractériser cette endomorphisme du plan vectoriel.
A +
Merci de ta réponse mais je comprends vraiment que dalle. C'est pourtant des maths, mais ce n est pas de mon niveau. MErci cependant d'avoir essayé de me faire comprendre...
Rebonjour,
J'aimerais bien comprendre cet exercice. Je rappelle la matrice
On doit déterminer les valeurs propres de f ainsi qu'un vecteur propre associé à chacune des valeurs propres de f.
Et pour terminer on doit donner une interprétation géométrique de cette application. Précédemment DHilbert, tu n'avais fait calculer On avait trouvé l'identité. Le déterminant est égal à -1. C'est donc un symétrie vectorielle. Ce que je voudrais savoir c'est comment déduire à partir des vecteurs propres et c'est une symétrie.
Je me lance je calculs les valeurs propres solutions de l'équation caractéristique Det ( M-  I) = 0
I) = 0
je trouve  =1 et
=1 et  =-1
=-1
Le vecteur propre associé à la valeur propre 1 est  = ( x, x)
= ( x, x)
Le vecteur propre associé à la valeur propre -1 est  = (x , (2/3)x)
= (x , (2/3)x)
Sauf erreur de ma part pour ces valeurs.
Ce que j'aimerais savoir c'est comment à partir de ces vecteurs propres, on peut caractériser cette application du plan ! Meme si on sait déja que c'est une symétrie vectorielle. Merci d'avance pour vos réponses !
je corrige l'expression :
Le sous-espace propre associé à la valeur propre 1 est l'ensemble des vecteurs pour
. Autrement dit, c'est la droite vectorielle engendrée par le vecteur
.
Je te laisse corriger ta petite erreur de calcul pour le deuxième sous-espace propre, associé à la valeur propre , et formuler le résultat comme je viens de le faire. Tu dois trouver une droite vectorielle engendrée par un vecteur
.
Soit l'application linéaire de matrice
. On a
et
.
Maintenant, si et
sont deux droites sécantes du plan, comment se comporte la symétrie d'axe
parallèlement à
? Ne peux-tu pas faire le rapport avec les droites vectorielles propres que tu as calculées ?
Bonsoir GabuZomeu,
merci de ta réponse.
Oui je me suis trompé pour le vecteur v. Après correction, je trouve que pour le deuxieme espace sous propre associé à la valeur propre -1, une droite vectorielle engendré par le vecteur v = (2,3). En passant que signifie droite vectorielle. Cela veut dire qu'elle ne passe pas par un point en particulier mais on sait juste par quel vecteur elle est engendrée ?
Concernant ta deuxième question, si on fait un petit dessin, on voit que l'application ne change pas le vecteur u, u est invariant donc par f. Je serais tenté de dire qu'il y a une symétrie axiale d'axe la droite engendré par le vecteur u ? Je n'en suis pas sur.
Merci de ton aide,
Une droite vectorielle, c'est un espace vectoriel de dimension 1, engendré par un vecteur non nul. Autrement dit, dans , une droite passant par l'origine.
Tu n'as pas clairement répondu à la question concernant la symétrie d'axe parallèlement à
. J'ai l'impression que pour toi, une symétrie est forcément une symétrie orthogonale. Est-ce le cas ?
D'accord pour la droite vectorielle. Oui en effet dans ma tête symétrie axiale = symétrie orthogonale. J'arrive pas vraiment à répondre à ta question...
Ok grâce à cette image j'ai pu comprendre... Donc cette application représente une symétrie vectorielle d'axe la droite dirigée par u parallèlement à la droite dirigée par v ?

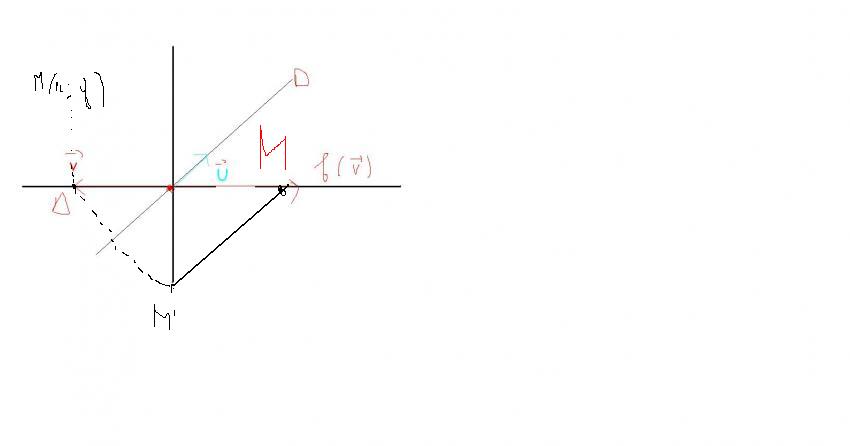

 en post-bac
en post-bac