Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale SimilitudesTopics traitant de similitudes [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

intersection de 3 cercles

Posté par
pppa 08-06-10 à 18:30

Bonjour à tous

Pouvez-vs m'aider à comprendre cet exercice svp.

Soit A,B et C 3 points non alignés du plan affine. A', B' et C' 3 points des droites (BC), (AC) et (AB).

Montrer que les cercles circonscrits aux triangles A'CB', B'AC' et C'BA' passent par un même point.

J'ai fait le schéma et on voit clairement cette intersection, mais je n'arrive pas à le démontrer.
Les centres des cercles circonscrits sont les points de concours des médiatrices des triangles correspondants, mais ça ne m'avance pas.

Merci de m'aider.

intersection de 3 cercles

Posté par
pppare : intersection de 3 cercles 08-06-10 à 18:32

Le point de (AC) qui n'est pas nommé c'est B'

Posté par
cailloux Correcteurre : intersection de 3 cercles 08-06-10 à 18:42

Bonjour pppa

Amusant, j' avais proposé cet exercice à propos des transformations ici: transformations

Pas beaucoup de succès...

Connais-tu les similitudes ?

Si oui, et si personne ne t' a répondu, je repasserai ce soir; je n' ai plus le temps maintenant...

Posté par
pppare : intersection de 3 cercles 08-06-10 à 18:52

Bonsoir Cailloux
Tiens, ça doit être un classique......mais qui n'a pas eu bcp de succès.

Dc je ressucite ton sujet et ton aide me sera la bienvenue. Oui, je connais un peu les similitudes, je vais qd même réviser avant que tu ne répondes pr essayer de mieux comprendre et + vite dtes réponses.

A + tard

Posté par
cailloux Correcteurre : intersection de 3 cercles 08-06-10 à 20:37

D' abord un préambule avec une figure et quelques résultats:

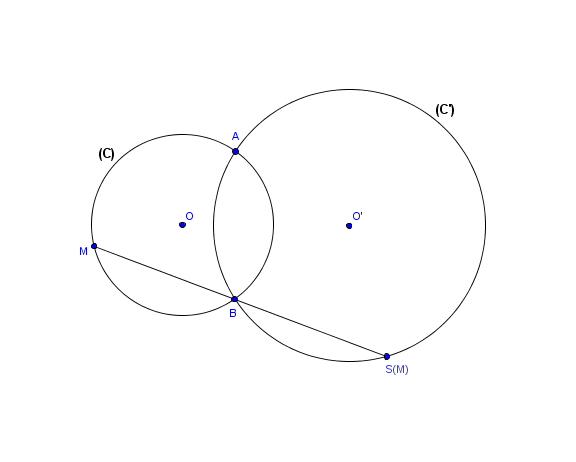
intersection de 3 cercles

Soit deux cercles (C) et (C') de centres O et O' sécants en A et B

Et soit S la similitude directe de centre A qui transforme O en O'

Alors:

- S[(C)]=(C')

- Pour tout point M de (C), M,B et S(M) sont alignés (avec S(M) point de (C'))

Ce résultat peut se démontrer avec les complexes; c' est un très bon exercice.
Si tu veux, je posterai la démonstration.

Puis une conséquence qu' on utilisera dans ton exercice:

Soit deux cercles (C) et (C') sécants en A et B et une sécante (MM') passant par B avec M\in (C) et M' \in (C'):

La similitude directe de centre A qui tranforme M en M' transforme (C) en (C')

Ton exercice avec une nouvelle figure:

intersection de 3 cercles

Les cercles (C_1) et (C_2) sont toujours sécants en 2 points distincts.

Appelons M le point d' intersection autre que C'

Soit S_1 la similitude directe de centre M qui transforme A en B

et S_2 la similitude directe de centre M qui transforme B en C

S_1 envoie C_1 sur C_2 (avec le préambule)

S_2 envoie C_2 sur C_3 (préambule itou).

Donc la similitude directe S_2\circ S_1 envoie C_1 sur C_3

Or S_2\circ S_1 est une similitude directe de centre M

donc M\in (C_3)



Posté par
pppare : intersection de 3 cercles 09-06-10 à 10:46

Bonjour Cailloux et merci pr ces explications détaillées.


C'est très bien vu la démonstration demandée par les similitudes. Dc ici, si je suis bien, ns sommes en présence de 2 similitudes directes distinctes mais de même centre M, chacune étant - apparemment - la composée d'une homothétie (manifestement de rapports positifs non nuls et différents de 1) et d'une rotation qui conserve les mesures d'angles orientés.


L'image d'un cercle par de telles similitudes directes est un cercle.

On définit une 1ère similitude directe dt le centre est un point d'intersection de 2 des 3 cercles, qui transforme le centre d'un des 2 cercles en le centre de l'autre cercle.

On considère ensuite une 2ème similitude directe de même centre qui transforme le centre du 1er cercle image en le centre du 3ème cercle.

La composée de 2 similitudes directes de  même centre est une similitude directe de même centre, et l'mage d'un cercle par ces similitudes directes est un cercle. Dc ce centre de similitudes - seul point invariant des 2 similitudes considérées - appartient nécessairement aux 3 cercles.

Est-ce que c'est correct comme interprétation de tes explications, même si c'est dit de manière + lourde et - limpide ?

Citation :


Ce résultat peut se démontrer avec les complexes; c' est un très bon exercice.
Si tu veux, je posterai la démonstration.
Oui je veux bien ; merci d'avance pr tes explications.

Bien cordialement

Posté par
cailloux Correcteurre : intersection de 3 cercles 09-06-10 à 13:37

Re bonjour,

Citation :
On définit une 1ère similitude directe dt le centre est un point d'intersection de 2 des 3 cercles, qui transforme le centre d'un des 2 cercles en le centre de l'autre cercle.


Non, non:

S_1 est la similitude directe de centre M qui transforme A en B

Et comme la sécante (AB) aux cercles (C_1) et (C_2) passe par C' second point d' intersection de ces cercles, S_1 envoie (C_1) sur (C_2) d' après la "conséquence" de 20h37

De même pour S_2

Pour le reste, tout va bien

La démonstration avec les complexes (que l' on peut trouver dans les (bons) bouquins de Terminale) avec la première figure de 20h37:

S est donc la similitude directe de centre A telle que S(O)=O'

- L' image par S du cercle (C) de centre O est donc le cercle de centre S(O)=O' passant par S(A)=A

C' est bien le cercle (C')

- On choisit un repère orthonormal d' origine O et d' axe réel (OO')

O' est d' affixe \omega réel.

A est d' affixe a et B est d' affixe \bar{a}

L' écriture complexe de S est alors:

z'=\left(1-\frac{\omega}{a}\right)z+\omega

En effet:

Il s' agit bien de l' écriture complexe d' une similitude directe.

Avec z=a, on a z'=a donc l' image de A est A

Avec z=0, on a z'=\omega donc l' image de O est O'

Soit M(z) un point de (C) et M'(z') son image par S:

On a: z_{\vec{BM}}=Z=z-\bar{a}

et z_{\vec{BM'}}=Z'=z'-\bar{a}

puis avec z\bar{z}=a\bar{a} (puisque M(z) appartient au cercle de centre O passant par A(a)):

3$\frac{Z'}{Z}=\frac{\left(1-\frac{\omega}{a}\right)z+\omega-\bar{a}}{z-\bar{a}}

3$\frac{Z'}{Z}=1+\omega\,\frac{1-\frac{z}{a}}{a-\bar{a}}

3$\frac{Z'}{Z}=1+\omega\,\frac{\left(1-\frac{z}{a}\right)\left(\bar{z}-a\right)}{|z-\bar{a}|^2}

3$\frac{Z'}{Z}=1+\omega \,\frac{\bar{z}-\frac{z\bar{z}}{a}-a+z}{|z-\bar{a}|^2}

3$\frac{Z'}{Z}=1+\omega\,\frac{z+\bar{z}-(a+\bar{a})}{|z-\bar{a}|^2} qui bien un réel.

Donc \vec{BM} et \vec{BM'} sont colinéaires.

et B,M,M' sont alignés.

Posté par
pppare : intersection de 3 cercles 09-06-10 à 18:22

Bonsoir Cailloux

donc si je comprends bien,

on considère au départ 2 des 3 cercles, et on définit une similitude directe S1 centrée en un des 2 points d'intersection des cercles, par laquelle l'image du centre du premier cercle est le centre du second.

et c'est parce que la sécante (M S1(M)) passe par B, deuxième point d'intersection des 2 cercles (sécants) considérés, que l'on peut conclure que l'image du premier cercle par S1 est le deuxième cercle considéré ?

J'avoue que je suis mal là ;j'aurais dit ceci (mais je ne pense pas avoir raison) : l'image d'un cercle par une similitude directe étant un cercle, la s.d. centrée en un point d'intersection de 2 cercles, et dt le centre d'un des cercles a pr image le centre de l'autre, est la s.d. par laquelle l'image du premier cercle est le 2ème cercle. Est-ce correct ou erroné ?

merici d'avance pr tex explications

Posté par
cailloux Correcteurre : intersection de 3 cercles 09-06-10 à 20:48

Bonsoir pppa,

Citation :
l'image d'un cercle par une similitude directe étant un cercle, la s.d. centrée en un point d'intersection de 2 cercles, et dt le centre d'un des cercles a pr image le centre de l'autre, est la s.d. par laquelle l'image du premier cercle est le 2ème cercle


C'est vrai(encore que l' article défini "la" n' est pas justifié: elle n' est pas unique) mais ici, on ne sait pas à priori que l' image du centre de l' un est le centre de l' autre:

Au départ, S_1 est définie comme la similitude directe de centre M telle que S(A)=B point final.

Mais comme la sécante (AB) aux deux cercles (C_1) et (C_2) passe par C' point d' intersection de ces 2 cercles autre que M, on peut affirmer que S[(C_1)]=(C_2) par application de la "conséquence" de 20h37:

Citation :
Soit deux cercles (C) et (C') sécants en A et B et une sécante (MM') passant B par avec M\in(C) et M'\in(C'):

La similitude directe de centre A qui tranforme M en M' transforme (C) en (C')


En adaptant les notations à l' exercice bien sûr.

Posté par
pppare : intersection de 3 cercles 09-06-10 à 23:29

Bonsoir Cailloux,

je remarque que tu insistes particulièrement sur la conséquence mentionnée ds ton message du 08 06 2010   20 h 37.
Et je pense que c'est là que j'ai une lacune qui fait que les explications ne sont pas (encore...) tt à fait claires pr moi.

En fait, ce que j'ai du mal à comprendre, c'est l'asserion suivante :

Citation :
Pour tout point M de (C) , M, B et S(M)  sont alignés (avec S(M) point de (C') ).


je ne parviens pas à comprendre prquoi la droite qui joint M et S(M) passe nécessairement par B ; je ne retrouve rien qui l'explique clairement ds les documents que j'ai consultés.

peux-tu m'expliquer + en détail stp.

merci par avance pr le tps que tu me consacres !

Posté par
cailloux Correcteurre : intersection de 3 cercles 09-06-10 à 23:50

Re,

Citation :
je ne parviens pas à comprendre prquoi la droite qui joint M et S(M) passe nécessairement par B ; je ne retrouve rien qui l'explique clairement ds les documents que j'ai consultés


Mais c' est précisément l' objet de la démo avec les complexes de 13h37!

Il y a d' ailleurs une fôte de frappe à la seconde ligne de calculs; il faut lire:

3$\frac{Z'}{Z}=1+\omega\,\frac{1-\frac{z}{a}}{z-\bar{a}}


Posté par
cailloux Correcteurre : intersection de 3 cercles 10-06-10 à 00:09

On en déduit aussi une méthode pour construire le centre d' une similitude directe définie par 4 points A,B,C,D

Soit A,B,C,D 4 points alignés tels que:

1) (AB) et (CD) soient sécantes en J

2) Les cercles circonscrits (C) et (C') aux triangles ACJ et BDJ se coupent en I

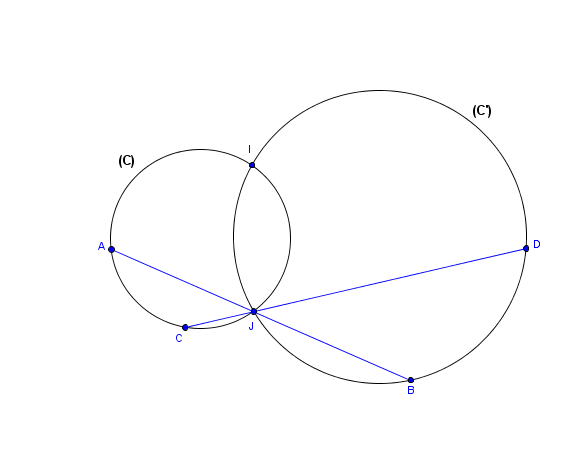
intersection de 3 cercles

Alors la similitude directe (unique) S qui transforme A en B et C en D est de centre I

Ces résultats ne sont pas au progamme de spé TS ...

Posté par
cailloux Correcteurre : intersection de 3 cercles 10-06-10 à 00:10

Euh ... soit A,B,C,D 4 points distincts bein sûr ...

Posté par
pppare : intersection de 3 cercles 10-06-10 à 18:53

Bonjour Cailloux

Pr la réponse à mon exercice j'ai bien tt compris et je te remercie.

J'ai juste une question complémentaire si tu permets : la composée de deux s.d. de même centre est une s.d. dt le centre est celui des similitudes composées, ça d'accord.

Par contre, comment détermine-t-on le centre de la composée de deux s.d. dt les centres sont distincts. Merci de me dire.


Pr la partie qui démontre l'alignement de 2 points (en relation par une s.d) de deux cercles sécants avec un des points d'intersection des 2 cercles,  j'en étais resté au point que tu as corrigé. Ca devrait aller mieux. je regarde.

merci

Posté par
cailloux Correcteurre : intersection de 3 cercles 10-06-10 à 22:09

Bonsoir pppa,

La question n' est pas simple pour une bonne raison:

La composée de deux similitudes directes n' est pas forcément une similitude à centre.

-Par exemple, la composée d' une similitude directe et de la similitude ditrecte réciproque est l' identité du plan.

-Ou bien si la composée est une translation (par exemple la composée h'\circ h de 2 homothéties de centres O et O' distincts de rapports k et \frac{1}{k} est une translation de vecteur \frac{1}{2}\vec{OO'})

En général, si on dispose des écritures complexes des 2 similitudes, on obtiendra sans difficulté l' écriture complexe de la composée. Si c' est une similitude à centre, ce centre sera le point invariant de cette composée.

On peut trouver ce centre géométriquement, par exemple ici dans le cas de la composée d' un homothétie et d' une translation:

Soit h une homothétie de centre O et de rapport k\not=1 et t une translation de vecteur \vec{u}

La composée t\circ h est une homothétie de centre \Omega et de rapport k telle que \vec{O\Omega}=\frac{1}{1-k}\vec{u}:

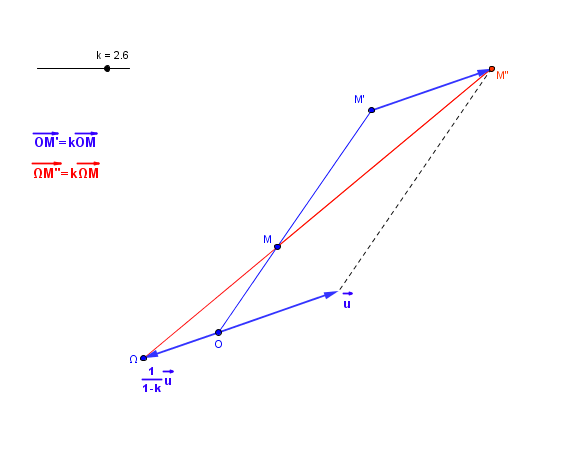
intersection de 3 cercles

Tu peux le prouver à titre d' exercice.

Autre exercice soit h et h' de centre O et O' distincts et de rapports k et k' tels que kk'\not= 1

Montrer que le centre de la composée est sur la droite (OO')

Tu l' auras compris: il n' y a pas vraîment de règle générale à part peut-être celle ci:

Toute similitude (directe ou indirecte) de rapport différent de 1 admet un unique point invariant.



Posté par
pppare : intersection de 3 cercles 10-06-10 à 23:58

Bonsoir cailloux

dans la démonstration de l'alignement des points M, B et M'(message du 09 06 2010 13 h 37), je ne comprends pas :

3$ z.\bar{z}=\alpha.\bar{\alpha} et comment on passe de :

3$\frac{Z'}{Z}=1+\omega.\frac{1-\frac{z}{\alpha}}{z-\bar{\alpha}}

à


3$\frac{Z'}{Z}=1+\omega.\frac{(1-\frac{z}{\alpha}).(\bar{z}-\alpha)}{|z-\bar{\alpha}|^2}. Est-ce que le nouveau facteur au numérateur ne serait pas plutôt  3$z-\bar{\alpha} plutôt que 3$\bar{z}-\alpha (3ème ligne de la démo).

Merci

Posté par
cailloux Correcteurre : intersection de 3 cercles 11-06-10 à 00:20

Je crois que tes 2 questions sont liées:

On a la formule générale: Z\bar{Z}=|Z|^2 (1)

Le cercle de centre O et de rayon OA est caractérisé par:

|z|=|a|

ou encore |z|^2=|a|^2

et avec (1):

z\bar{z}=a\bar{a} ( M(z) et A(a) appartiennent tous deux au cercle de centre O et de rayon OA)

Pour la suite:

3$\frac{Z'}{Z}=1+\omega.\frac{1-\frac{z}{\alpha}}{z-\bar{\alpha}}

Dans la fraction, on multiplie haut et bas par 3$\bar{z}-a:

3$\frac{Z'}{Z}=1+\omega\,\frac{\left(1-\frac{z}{a}\right)(\bar{z}-a)}{(z-\bar{a})(\bar{z}-a)}

Or au dénominateur:

3$(z-\bar{a})(\bar{z}-a)=(z-\bar{a})\overline{(z-\bar{a})}=|z-\bar{a}|^2 (toujours avec (1))


et 3$\frac{Z'}{Z}=1+\omega.\frac{(1-\frac{z}{\alpha}).(\bar{z}-\alpha)}{|z-\bar{\alpha}|^2}







Posté par
pppare : intersection de 3 cercles 11-06-10 à 18:54

Bonjour
Cailloux

Globalement je pense avoir compris la démonstration de l'alignement des points M, B et M' par les nbres cplx : le rapport des 2 nbrs cplx Z' et Z est un nbre réel ; Z et Z' sont les affixes des vecteurs \vec{BM} et \vec{BM'} ( écrits resp.
3$z_{\vec{BM}} et 3$z_{\vec{BM'}} (je precise ça pr être sûr car au début j'avais un doute sur cette écriture, dc si c'est pas ça dis le moi stp).

On démontre que le rapport \frac{Z'}{Z} est un nbre réel, ce qui prouve que les 2 vecteurs dt on a calculé le rapport des affixes sont colinéaires.

Il reste que , malgré tes explications d'hier soir, (ou de très tôt ce matin), je ne comprends pas l'écriture

3$(z-\bar{\alpha}).(\bar{z}-\alpha)=(z-\bar{\alpha}).\bar{(z-\bar{\alpha})}=|z-\bar{\alpha}|^2. je dois avoir qqs lacunes sur ces manipulations de nbrs cplx ; peut tu m'éclairer stp. Merci d'avance.

Posté par
Yzzre : intersection de 3 cercles 11-06-10 à 19:04

Salut Philippe, tu vas bien?  
Je m'immisce juste sur ton topic, pour une réponse à ta dernière question:

Pour tout complexe z, on a : z.z(barre)= /z/²  (Tu peux le prouver aisément en posant z=a+ib)
et
Le conjugué du conjugué de Z est égal à Z : c'est ce qu'a utilisé cailloux pour remplacer z-(barre) par (z-(barre))(barre)
Faudra bien que je m'y mette, au LaTex...

Posté par
Yzzre : intersection de 3 cercles 11-06-10 à 19:05

Rectif dernière ligne:
c'est ce qu'a utilisé cailloux pour remplacer z(barre)- par (z-(barre))(barre)

Posté par
pppare : intersection de 3 cercles 11-06-10 à 23:01

Bonsoir Géraud,

ça va bien je te remercie, sauf que je pédale un peu à vide avec ces nbres cplx appliqués aux similitudes.

Citation :

Je m'immisce juste sur ton topic,
mais tu es le bienvenu, et je ne pense pas que Cailloux s'offusquera de ton intervention.


Citation :
Pour tout complexe z, on a : z.z(barre)= /z/²
Ca OK (qd même)

Citation :
Le conjugué du conjugué de Z est égal à Z :
Oui, ça aussi

Mon pb (je suis persuadé que qd on va m'expliquer je vais me foutre des baffes, mais pr l'instant je bloque tjs) c'est que je ne comprends pas comment on passe de 3$(\bar{z}-\alpha), à 3$(z-\bar{\alpha}) ( pr en prendre ensuite le conjugué).

Le conjugué de a + ib, c'est a - ib, alors je me dis .....

Ah je crois que je viens de comprendre : z et sont des complexes qui s'écrivent déjà ss la forme a + ib pr z et - i pr \bar{\alpha} par ex.

Dc 3$z-\bar{\alpha}=(a+ib)-(\lambda-i\mu)=(a+ib)-\lambda+i\mu=(a-\lambda)-i.(b+\mu)=a-ib-\lambda-i\mu=(a-ib)-(\lambda+i\mu)=\bar{z}-\alpha. C'est ça ? ça me parait tenir la route et me permet de comprendre la démonstration, enfin je pense

Posté par
cailloux Correcteurre : intersection de 3 cercles 11-06-10 à 23:36

Bonsoir pppa,

Bien sûr que Yzz est le bienvenu! La question ne se pose pas

Ta dernière ligne est fausse; tu as écrit qu' un complexe est égal à son conjugué: ce n' est vrai que s' il est réel

Je crois que ton souci vient d' une difficulté à manipuler l' opérateur "conjugué".

Avec cet opérateur, tout est permis; en vrac:

\overline{z+z'}=\bar{z}+\bar{z'} (le conjuqué d' une somme (ou d' une différence) est la somme des conjugués).

\overline {zz'}=\bar{z}\,\bar{z'} (le conjugué d' un produit est le produit des conjugués).

\overline{\left(\frac{z}{z'}\right)}=\frac{\bar{z}}{\bar{z'}} (le conjugué d' un rapport est le rapport des conjugués).

\overline{(z^n)}=(\overline{z})^n (le conjugué d' une puissance est la puissance du conjugué)

\overline{\bar{z}}=z (le conjugué du conjugué est le complexe lui même).

Maintenant, on va prouver que:

\overline{z-\bar{a}}=\bar{z}-a:

\overline{z-\bar{a}}=\overline{z}-\overline {\bar{a}} (avec la règle sur le conjugué d' une somme ou d' une différence).

\overline {z-\bar{a}}=\bar{z}-a (avec la dernière règle).

Pour la suite, on a donc:

(z-\bar{a})(\bar{z}-a)=(z-\bar{a})\overline{(z-\bar{a})}=|z-\bar{a}|^2

Est-ce plus clair ?

Posté par
pppare : intersection de 3 cercles 13-06-10 à 09:42

Bonjour Cailloux

excuse-moi je ne reviens que maintenant sur le sujet (hier j'étais entre autres occupé avec un sujet qui m'a pris plus de tps que prévu).

A la lumière de tes explications, et en particulier celles d'avant hier soir, j'ai refait tt seul et compris de bout en bout le démonstration de l'alignement des points M, B et M'.

Merci de m'avoir comblé mes lacunes.

Il me reste à étudier ce que tu m'as écrit sur la composition des similitudes de centres distincts. Si besoin je me permettrai de te poser des questions complémentaires si tu permets.

Merci encore et à bientôt .

très cordialement

Posté par
cailloux Correcteurre : intersection de 3 cercles 13-06-10 à 13:05

Alors tout va bien

Juste une rectification:

A la fin de 22h09, j' ai oublié de préciser que h et h' étaient 2 homothéties de centre O et O'

A bientôt

Posté par
pppare : intersection de 3 cercles 14-06-10 à 18:47

Bonjour Cailloux !

Citation :
A la fin de 22h09, j' ai oublié de préciser que h et h' étaient 2 homothéties de centre O et O'


Non je n'a pas eu de doute à ce sujet en lisant ce message. Je souhaite par contre si tu permets qqs explications complémentaires.

Je suis sur le 1 er exemple :  
Citation :
la composée est une translation (par exemple la composée h' o h de 2 homothéties de centres O et O' distincts de rapports k et 1/k est une translation de vecteur \frac{1}{2}\vec{OO'}
.

J'essaie de le démontrer.

Soit M1 l'image de M par h. 2$h(M)=M_1\Leftrightarrow\vec{OM_1}=k.\vec{OM}

Soit M' l'image de M1 par h'. 2$h'(M_1)=M'\Leftrightarrow\vec{O'M'}=\frac{1}{k}.\vec{O'M_1}

L'image de M par la composée h' o h serait : (h' o h)(M) = h'[h(M)] = h'(M1)=M', soit :

3$\vec{O'M'}=\frac{1}{k}\vec{O'M_1}=\frac{1}{k}.(\vec{O'O}+\vec{OM_1})=\frac{1}{k}.\vec{O'O}+\vec{OM}.

J'en suis là ; je n'arrive pas à montrer que cette composition des 2 homothéties est la translation de vecteur \frac{1}{2}\vec{OO'}.

Peux-tu m'aider stp.

D'avance merci

Posté par
cailloux Correcteurre : intersection de 3 cercles 14-06-10 à 19:13

Au temps pour moi, j' avais écrit n' importe quoi et tu n' avais aucune chance.

Il faut démontrer que h'\circ h est une translation de vecteur \frac{k-1}{k}\,\vec{OO'}

Avec ceci:

Citation :
3$\vec{O'M'}=\frac{1}{k}.\vec{O'O}+\vec{OM}


tu es tout près du résultat

Posté par
cailloux Correcteurre : intersection de 3 cercles 14-06-10 à 19:14

Et bonsoir pppa

Posté par
pppare : intersection de 3 cercles 14-06-10 à 23:15

Bonsoir Cailloux

Ah oui, ça semble aller mieux.

de ma dernière étape, il vient :

3$\vec{O'M'}=-\frac{1}{k}\vec{OO'}+\vec{OO'}+\vec{O'M}

3$\vec{O'M'}-\vec{O'M}=(1-\frac{1}{k}).\vec{OO'}

3$\vec{MM'}=(\frac{k-1}{k}).\vec{OO'}

avec M' = (h' o h)(M). La composée de ces 2 homothéties est dc bien la translation de vecteur 3$(\frac{k-1}{k}).\vec{OO'}


Merci et bonne nuit !

  (je te rassure,j'y ai pas passé la soirée, j'ai repris le topic vers 23 h 00)

Posté par
pppare : intersection de 3 cercles 15-06-10 à 19:03

Bonjour Cailloux,

Citation :
On peut trouver ce centre géométriquement, par exemple ici dans le cas de la composée d' un homothétie et d' une translation:

Soit h une homothétie de centre O et de rapport k et t une translation de vecteur
.

Soit M un point du plan affine ; M' son image par h. On a : 3$h(M)=M'\Leftrightarrow\vec{OM'}=k.\vec{OM}.

On pose M" = t(M'). On a : 3$t(M')= M_1 \Leftrightarrow\vec{M'M_1}=\vec{u}.


Il s'agit donc de trouver la transformation (t o h) qui au point M associe M1.

Ma 1ère question : . comment sait-on que c'est une homothétie ?

On a : 3$\vec{M'O}+\vec{OM_1}=\vec{u}

3$k.\vec{MO}+\vec{OM_1}=\vec{u}

3$\vec{OM_1}=k\vec{OM}+\vec{u}

J'en suis là ; peux-tu m'aider à avancer pr achever la démonstration stp.

merci

Posté par
cailloux Correcteurre : intersection de 3 cercles 15-06-10 à 19:34

Bonjour pppa,

Citation :
Ma 1ère question : . comment sait-on que c'est une homothétie ?


J' aurais du préciser k\not=\pm 1

h(O,k) est une similitude directe de rapport |k|

et t_{\vec{u}} est une similitude directe de rapport 1

Donc t\circ h est une similitude directe de rapport |k|

Commme |k|\not =1, t\circ h est une similitude directe qui n'est pas une isométrie du plan.

C' est donc une homothétie.

Citation :
3$\vec{OM_1}=k\vec{OM}+\vec{u}


Tout à fait; il te reste à chercher sont point invariant:

M=M_1

Tu pourras examiner ensuite ce qui se passe pour k=-1

Posté par
pppare : intersection de 3 cercles 15-06-10 à 23:48

Bonsoir Cailloux

ds mon message de 19 h 03, j'ai changé en cours de messahge M" en M1 car le symbole " ne passait en latex, non plus que 2 fois '...Je pense que tu m'auras suivi qd même.

Dc (t o h)(M) m'aura conduit à l'égalité vectorielle : 3$\vec{OM_1}=k.\vec{OM}+\vec{u}.

En cherchant le point invariant de cette transformation, j'aboutis effectivement à :
\vec{OM}=\frac{1}{1-k}.\vec{u}, ce qui donne l'expression génrale de cette composition de déplacements dans le plan.

Pr k = -1, on a : \vec{OM}=\frac{1}{2}.\vec{u}. Qu'en conclure de particulier?

Posté par
cailloux Correcteurre : intersection de 3 cercles 16-06-10 à 11:33

Bonjour pppa,

Pour k\not=\pm 1 on peut préciser les choses:

On a donc un point invariant \Omega défini par \vec{O\Omega}=\frac{1}{1-k}\vec{u}

Du coup (avec mes notations):

\vec{\Omega M''}=\vec{\Omega M}+\vec{MO}+\vec{OM'}+\vec{M'M''}

\vec{\Omega M''}=\vec{\Omega M}+(k-1)\vec{OM}+\vec{u}

\vec{\Omega M''}=\vec{\Omega M}+(k-1)\vec{OM}+(1-k)\vec{O\Omega}

\vec{\Omega M''}=k\vec{\Omega M}

On retrouve bien que t\circ h une l' homothétie de centre \Omega mais on a en plus son rapport: k

Si k=-1, on a une symétrie centrale de centre \Omega:

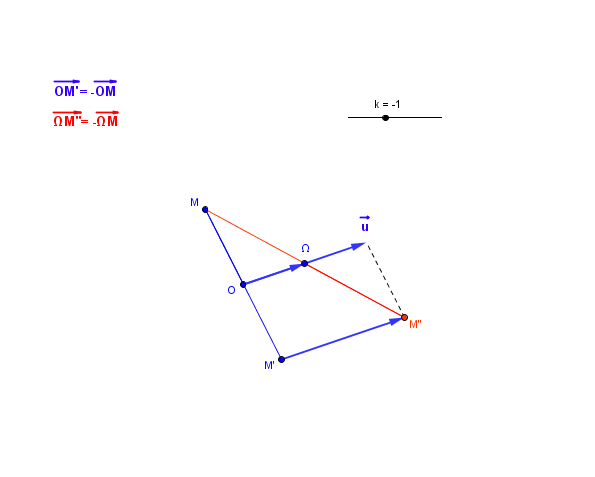
intersection de 3 cercles

Posté par
pppare : intersection de 3 cercles 16-06-10 à 21:28

Bonsoir Cailloux

merci pour tes explications de ce matin que j'ai bien compris.

Il me reste à  traiter sur ce sujet :

Citation :
soit h et h' de centre O et O' distincts et de rapports k et k' tels que kk' 1.


Montrer que le centre de la composée est sur la droite (OO')


Je n'ai pas abouti. Voilà ce que j'ai fait :

Soit h l'homothétie de centre O et de rapport k, telle que : h(M)=M1 ; on a : 3$\vec{OM_1}=k.\vec{OM}.

Soit h' l'homothétie de centre O' et de rapport k', telle que : h'(M)=M' ; on a : 3$\vec{O'M'}=k'.\vec{O'M}..

(h' o h)(M) = h'[h(M)] = h'(M1) = M2 ; soit : 3$\vec{O'M_2}=k'.\vec{O'M_1}=k'.[\vec{O'O}+\vec{OM_1}]=k'.\vec{O'O}+kk'.\vec{OM}.

soit : 3$\vec{O'M_2}-k'.\vec{O'O}=kk'.\vec{OM}

3$\vec{O'M_2}-\vec{O'O}-(k'-1).\vec{O'O}=kk'.\vec{OM}
soit
3$\vec{OM_2}=kk'.\vec{OM}+(k'-1).\vec{O'O}

Peux-tu me dire si j'ai pris la bonne voie et m'aider à finaliser stp

D'avance merci.

Posté par
cailloux Correcteurre : intersection de 3 cercles 16-06-10 à 22:14

Bonsoir pppa,

Tu t 'es arrêté au même endroit qu' à 19h03.

On a donc 3$\vec{OM_2}=kk'.\vec{OM}+(k'-1).\vec{O'O}

et on cherche les éventuels points invariants:

c' est à dire M_2=M

On obtient un unique point \Omega défini par:

\vec{O\Omega}= \frac{k'-1}{1-kk'}\vec{OO'} pour kk'\not=1

Ce qui signifie bien que \Omega \in (OO')

On peut montrer ensuite que \vec{\Omega M_2}=kk'\vec{\Omega M}

Donc que h'\circ h est l' homothétie de centre \Omega et de rapport kk'

Si kk'=1, la composée est une similitude directe de rapport 1 donc une rotation ou une translation. On montre que c' est une translation.

Posté par
pppare : intersection de 3 cercles 17-06-10 à 21:54

Bonsoir Cailloux

j'ai retravaillé ce soir sur tes dernières explications. J'ai clairement établi qu'il existe un unique point invariant par la composée (h' o h).

Je pense que si je me suis à nouveau arrêté en chemin ds la démo, c'est parce qu'il y a qqc qui n'est pas (encore) tt à fait clair ds mon esprit sur ce  sujet, mais je pense que tu vas m'aider à clarifier ça.

Je cherchais le CENTRE de la composée de ces 2 homothéties, connaissant leurs rapports resp. J'applique dc la définition de l'homothétie...

Ce qui n'est pas (encore) évident pr moi, c'est que la recherche du centre d'une homothétie (ou de la composition d'homothéties), se fasse en recherchant le ou les points invariants par cette transformation. Est-ce la méthode systématique pr faire cette démonstration ?

par ailleurs j'ai essayé d'établir que  3$\vec{\Omega M_2}=kk'.\vec{\Omega M}.

En posant 3$\vec{\Omega M_2}=\vec{\Omega O}+\vec{OO'}+\vec{O'M_2}, j'aboutis à 3$\vec{\Omega M_2}=kk'.\vec{O'M}.

Où est la faille ? Veux-tu le détail de ma démo ?

Merci pr le tps que tu me consacres !

Posté par
cailloux Correcteurre : intersection de 3 cercles 17-06-10 à 22:30

Bonsoir pppa,

Citation :
Je cherchais le CENTRE de la composée de ces 2 homothéties, connaissant leurs rapports resp. J'applique dc la définition de l'homothétie...

Ce qui n'est pas (encore) évident pr moi, c'est que la recherche du centre d'une homothétie (ou de la composition d'homothéties), se fasse en recherchant le ou les points invariants par cette transformation. Est-ce la méthode systématique pr faire cette démonstration ?


Lorsqu' on cherche la nature de la composée de 2 homothéties qui est la composée de 2 similitudes directes, on sait déjà qu' il s' agira d' une similitude directe.

D' où la question qu' on peut se poser naturellement:

Est-ce une similitude directe à centre ?

Si oui, on élimine les translations. Si non, on a affaire à une translation (j' élimine l' identité du plan qui est aussi possible dans des cas très particuliers).

D' où l' intérêt de la recherche de cet éventuel point invariant.

Et s' il s' agit d' une homothétie, ce point invariant est le centre de cette homothétie.

Citation :
En posant 3$\vec{\Omega M_2}=\vec{\Omega O}+\vec{OO'}+\vec{O'M_2} j' aboutis à 3$\vec{\Omega M_2}=kk'.\vec{O'M}


Tu as sûrement une petite boulette quelque part...

Posté par
pppare : intersection de 3 cercles 18-06-10 à 13:16

Bonjour Cailloux.

Ca y est j'ai établi la démonstration : 3$\vec{\Omega M_2}=kk'.\vec{\Omega M}.
Effectivement il y avait un petit pb mais je crois (j'aimerais si possible que tu vérifies pr que je valide définitivement cette démo) que ça venait de ce que j'ai repris

3$\vec{O\Omega}=\frac{k'-1}{1-kk'}.\vec{OO'} alors qu'il semblerait que ce soit - à ce niveau -

3$\vec{O\Omega}=\frac{k'-1}{1-kk'}.\vec{O'O} (Cf ton message du 16/06/2010 - 22h14).



Citation :
Si , la composée est une similitude directe de rapport 1 donc une rotation ou une translation. On montre que c' est une translation.


Pr kk'=1, on a dc 3$\vec{\Omega M_2}=\vec{\Omega M}, soit M2 confondu avec M.

Sachant que (h' o h)(M) = M2, n'est-on pas en présence de l'identité du plan affine ?

Merci de me dire, et je crois que ns en aurons alors fini avec ce sujet, sauf nouvelles interrogations et si tu es disponible.

Posté par
cailloux Correcteurre : intersection de 3 cercles 20-06-10 à 12:28

Bonjour pppa,

Il y a effectivement une erreur de signe à 22h14; il s' agit de :

\vec{O\Omega} =\frac{1-k'}{1-kk'}\vec{OO'}

Si kk'=1, à partir de \vec{OM_2}=kk'.\vec{OM}+(k'-1).\vec{O'O} tu dois normalement aboutir à:

\vec{MM_2}=\frac{k-1}{k}\vec{OO'} ou \vec{MM_2}=(1-k')\vec{OO'}

Posté par
pppare : intersection de 3 cercles 21-06-10 à 20:15

Bonsoir Cailloux

\vec{OM_2}=kk'.\vec{OM}+(k'-1).\vec{O'O}

Pr kk'=1, on a \vec{OM_2}=\vec{OM}+(k'-1).\vec{O'O}



\vec{OM}+\vec{MM_2}=\vec{OM}+(k'-1).\vec{O'O}



\vec{MM_2}=(k'-1).\vec{O'O}



\vec{MM_2}=(1-k').\vec{OO'}

Bien sûr. On est dc bien en présence d'une translation.....je peux conclure en disant

translation d'un vecteur colinéaire au vecteur joignant les 2 centres des homothéties dans le sens inverse de la composition h' o h : h' est composée avec h, tandis que la transalation de vecteur \vec{OO'} est dirigée du centre de h vers celui de h'.
Est-ce la bonne conclusion ?

Merci de me dire

Posté par
cailloux Correcteurre : intersection de 3 cercles 22-06-10 à 00:12

Bonsoir pppa,

Oui, mais il est inutile de vouloir préciser l' orientation du vecteur translation.

Ce sens dépend de k' (ou de k)...

Posté par
pppare : intersection de 3 cercles 22-06-10 à 18:04

Très bien ; grand merci. Sujet terminé pr moi.

Posté par
cailloux Correcteurre : intersection de 3 cercles 22-06-10 à 20:58


Rechercher
Menu
Espace membre
14 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1741 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !