Inscription / Connexion Nouveau Sujet
Intervalle
Bonjour,
j'ai un exercice sur les intervalles, mais je ne comprend strictement rien.
J'ai réussi à trouver quelques réponses, mais je ne sais pas si elle sont correct ou non.
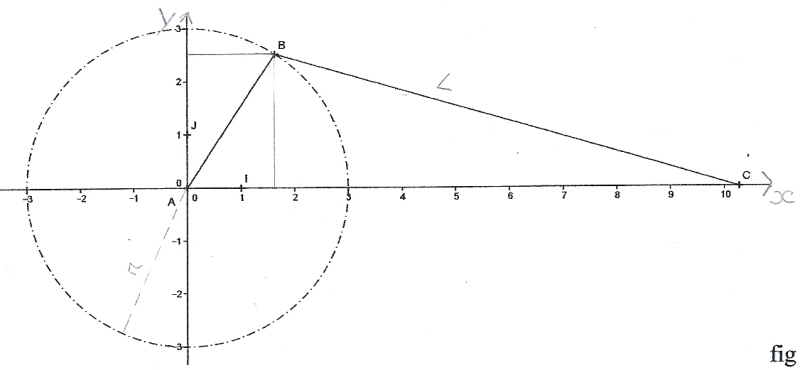
Voir figure ci dessous.
2. Trouvez le(s) intervalle(s) des coordonées xb et yb du point B.
Réponse : xb = 1.6 ; yb = 2.4 Intervalle [1.6;2.4] Correct ?
3. Trouvez l'intervalle de l'abscisse xc du point C.
Quel est sont signe.
Réponse : xc = 10.3 Intervalle [0;10.3]
Signe de xc = Signe positif
4. On suppose que B(0 ;r), exprimer en fonction de L et r les coordonées du point C.
Réponse : r = 2.9 cm ( r + L ) = 11.5 (Je sais que j'ai faux ..)
L = 8.6 cm
5. On suppose que xb = r/racine carré et que yb >0.
Réponse : xb = 2.9/ racine carré et yb > 0 donc xb = 2.050609665. (exercice pas fini..)
5.b) En déduire xc en fonction de L et r.
Réponse : Pas trouvé.
5.c) Faire une figure en prenant r = 3cm et L = 9cm. Donner une valeur approchée des coordonées des points B et C.
Bonjour, donner un intervalle ce n'est pas donner les coordonnées d'un point...
De plus je pense que l'énoncé n'est pas complet:
on ne sait pas grand chose sur la position de B et C...
N'y aurait il pas une phrase disant que le point B appartient au cercle de rayon et de centre (0,0)?
Et que le point C appartient à l'axe des abscisses?
Et que la longueur BC = L est constante?
Précisément?
B appartient il au cercle ou seulement à un quart ou un demi cercle?
Quoi qu'il en soit, l'abscisse de B ne pourra jamais être 2...
Entre quelles valeurs peuvent être comprise l'abscisse et l'ordonnée de B?
La phrase exact est :
A est fixe.
B décrit le cercle de centre A et de rayon r.
C se déplace sur l'axe (OI), la longueur L du segment [BC] étant constante.
L > r
Les intervalles recherché sont :
- intervalle des coordonnées xb et yb du point B.
- l'intervalle de l'abscisse xc du point C.
Merci de ton aide 
J'avais compris, masi je te demande des valeurs, xb ne peux pas prendre certaine valeur...
si xb = 2, le point B ne sera plus sur le cercle.
Quelles sont donc l'ensemble des valeurs que peuvent prendre xb,yb et xc?[sub][/sub]
Mais on ne te demande pas une lecture graphique des coordonnées d'un point!
Le point B n'est pas forcément là où il est représenté sur le schéma, mais il peut être n'importe où sur le cercle!
Est ce que tu sais ce qu'est un intervalle? C'est comme même une notion essentielle...
s xb est strictement supérieur à 1, B ne peux pas faire partie du cercle.
De même si xb est strictement inférieur à -1.
Par contre, si xb est compris entre -1 et 1, B peux faire partie du cercle...
L'ensemble des valeurs possibles pour xb est donc l'intervalle [-1,1]
Je te laisse faire la suite...


