Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Géometrie plane et dans l'espaceTopics traitant de Géometrie plane et dans l'espace [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Isométries (Composée de rotation)

Posté par
matheux14 09-05-21 à 23:14

Bonjour ,

Merci d'avance.

Dans le plan orienté, on considère un triangle ABC direct.
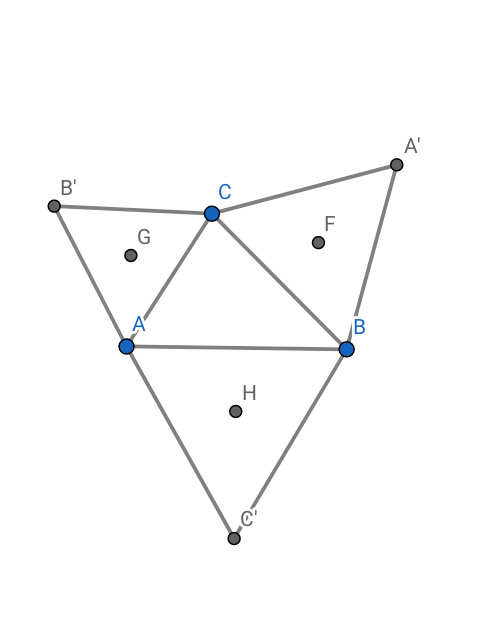
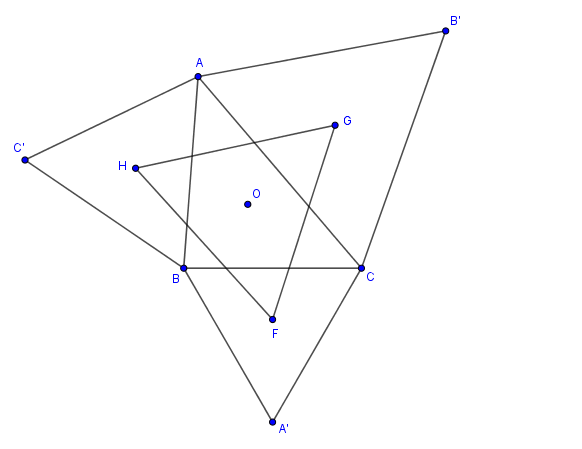
1. Construire les triangles équilatéraux directs A'CB , B'AC et C'BA de centres respectifs F, G et H.

Isométries (Composée de rotation)

Réponses

1) Isométries (Composée de rotation)

2-a) r_1 \circ r_2 est la composée de deux rotations de centres différents.

==> r_1 \circ r_2 est soit une symétrie centrale soit une rotation.

2-b) f(B)=r_1 \circ r_2 \circ r_3 (B)=r_1 \circ r_2 [r_3 (B)]=r_1 \circ r_2(A)=r_1(C)=B

f(B)=B

2-c) f(B)=B ==> f=Idp

2-d) f=Idp ==> r_1 \circ r_2 \circ r_3=Idp

==> r_2 \circ r_3=r_1^{-1}

3) J'ai pris \vec{u} et \vec{GH} les vecteurs directeurs unitaires de (D1) et (GH). Mes(\vec{u} ;\vec{GH})=\dfrac{2\pi}{3}.

Ensuite je bloque..

Posté par
lakere : Isométries (Composée de rotation) 09-05-21 à 23:35

Bonsoir,

Commençons par 2)a) :

  

Citation :
==> r_1 \circ r_2 est soit une symétrie centrale soit une rotation.


Beaucoup à dire :

  - et si la somme des angles vaut 0 modulo 2\pi ?
  - une symétrie centrale est une rotation d'angle \pi. Il n'y a pas lieu de faire de différence.
   - le plus important : il faut préciser : une rotation ? quel angle et quel centre ?

Posté par
matheux14re : Isométries (Composée de rotation) 09-05-21 à 23:44

D'accord , je croyais que c'était les éléments caractéristiques tout ça ..

Posté par
lakere : Isométries (Composée de rotation) 09-05-21 à 23:46

"D'accord" ça ne suffit pas :

Citation :
- le plus important : il faut préciser : une rotation ? quel angle et quel centre ?


?

Posté par
matheux14re : Isométries (Composée de rotation) 10-05-21 à 00:00

Le centre de r2or3 est le point d'intersection des droites (D) et (D') telles que (D)=R(F ; π/3)(GH) et (D')=R(G ; -π/3)(GH).

L'angle de est égal à 4π/3

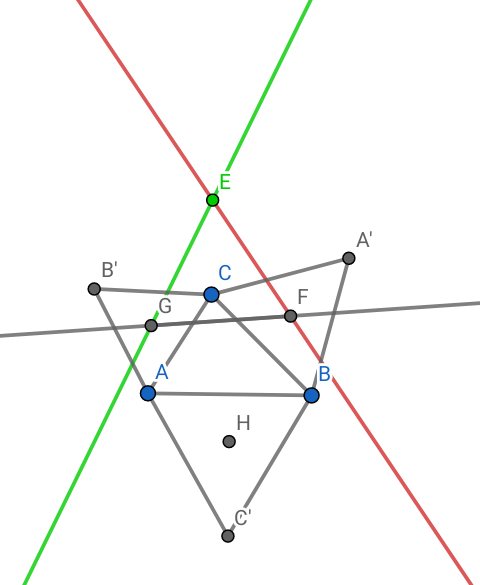
Isométries (Composée de rotation)

Posté par
lakere : Isométries (Composée de rotation) 10-05-21 à 00:05

Pour l'angle, d'accord. Note au passage que modulo 2\pi, il vaut aussi -\dfrac{2\pi}{3}. (Il faudra t'en souvenir un peu plus tard).

Pour le centre, tu t'es trompé.

Peux-tu déterminer l'image de A par r_1\cir r_2 ?

Posté par
lakere : Isométries (Composée de rotation) 10-05-21 à 00:06

zut :

  ... par r_1\circ r_2 ?

Posté par
matheux14re : Isométries (Composée de rotation) 10-05-21 à 00:13

Ah désolé , j'ai fait r2 o r3 au lieu de r1 o r2.

Posté par
lakere : Isométries (Composée de rotation) 10-05-21 à 00:16

Peut-être, mais peux-tu répondre à la question :

  

Citation :
Peux-tu déterminer l'image de A par r_1\circ r_2 ?


Elle a son importance !

Posté par
matheux14re : Isométries (Composée de rotation) 10-05-21 à 00:25

Le point A'2 sur la figure.Isométries (Composée de rotation)

Posté par
lakere : Isométries (Composée de rotation) 10-05-21 à 00:30

Pas du tout; il est parfaitement inutile de faire un dessin :

r_1\circ r_2(A)=r_1[r_2(A)]

r_2(A)=?

puis r_1(?)=??

Posté par
lakere : Isométries (Composée de rotation) 10-05-21 à 00:33

Je vois que tu as inversé l'ordre de composition.

Posté par
matheux14re : Isométries (Composée de rotation) 10-05-21 à 00:36

Ah oui , c'est le point B

Posté par
lakere : Isométries (Composée de rotation) 10-05-21 à 00:39

Oui

donc r_1\circ r_2 est la rotation d'angle -\dfrac{2\pi}{3} qui envoie A sur B

Elle est parfaitement définie ; quel est son centre ?

Il suffit de regarder la figure...

Posté par
matheux14re : Isométries (Composée de rotation) 10-05-21 à 00:43

La rotation de centre H et d'angle -2π/3

Posté par
lakere : Isométries (Composée de rotation) 10-05-21 à 00:51

Oui!

Et donc r_1\circ r_2=r_3^{-1} puisque r_3 est la rotation de centre H et d'angle {\red +}\dfrac{2\pi}{3}

et de  r_1\circ r_2=r_3^{-1}, on déduit immédiatement que :

f=r_1\circ r_2\circ r_3=Id

Pour moi, c'est cela l'ordre des choses.

Évidemment tu as 2)b) et 2)c) qui fichent mon "ordre" par terre. Mais je préfère ma méthode

Il faut que je dorme...

Bonne nuit !

Posté par
matheux14re : Isométries (Composée de rotation) 10-05-21 à 00:57

Bonne nuit à vous

Posté par
lakere : Isométries (Composée de rotation) 10-05-21 à 01:08

Juste avant de dormir;

Cette question 2)a) ne me plait pas :

Citation :
2)a) Déterminer la nature de...


Sous le vocable « nature », on peut mettre tout et n'importe quoi ...
C'est ce qui m'a incité à prendre quelques libertés avec ton énoncé.

Posté par
matheux14re : Isométries (Composée de rotation) 10-05-21 à 08:17

Ah d'accord.

Pour la question 3) Je ne vois pas vraiment..

Posté par
lakere : Isométries (Composée de rotation) 10-05-21 à 10:08

3)a) Tu sais faire : des compositions de symétries axiales pour obtenir des rotations.

Posté par
lakere : Isométries (Composée de rotation) 11-05-21 à 13:28

Bonjour,

Je reviens sur 2)a)b)c)d) qu'on a traité à "ma manière" sans se préoccuper de l'énoncé.
En le suivant pas à pas :

  2)a) La somme des angles des rotations r_1 et r_2 vaut \dfrac{4\pi}{3}\equiv -\dfrac{2\pi}{3}\;\;[2\pi] (somme non nulle modulo 2\pi).

    r_1\circ r_2 est donc une rotation d'angle -\dfrac{2\pi}{3}

  Pour f, la somme des angles est nulle modulo 2\pi. f est donc une translation.

2)b) Il est facile de montrer que f(B)=B

2)c) f est donc une translation de vecteur nul : f=\text{Id}_P

2)d) Du coup, r_2\circ r_3=r_1^{-1} c'est à dire la rotation de centre F et d'angle -\dfrac{2\pi}{3}

Ceci pour arriver à 3)a) où on te demande de "construire" .
Je te le répète : tu sais faire.

Un petit dessin est attendu ...

Posté par
mathafou Moderateurre : Isométries (Composée de rotation) 12-05-21 à 15:12

Bonjour,

... le bicentenaire est fini, l'exo est abandonné à Sainte-Hélène ?
( pas pu m'en empêcher .. : cet exo démontre le "théorème de Napoléon")

Posté par
lakere : Isométries (Composée de rotation) 12-05-21 à 16:40

Bonjour mathafou,



Tout de même : matheux14 n'est pas du genre à "abandonner" ses sujets. Il peut avoir des absences mais en général il revient toujours

Posté par
matheux14re : Isométries (Composée de rotation) 13-05-21 à 11:03

Citation :
... le bicentenaire est fini, l'exo est abandonné à Sainte-Hélène ?


Je n'abandonne pas mes topics moi ..

Posté par
lakere : Isométries (Composée de rotation) 13-05-21 à 11:34

Bonjour matheux14,

Donner signe de vie, c'est bien.
Continuer ton exercice, c'est mieux

Posté par
matheux14re : Isométries (Composée de rotation) 13-05-21 à 11:56

D'accord mais j'aimerais bien terminer l'autre exo.

Posté par
matheux14re : Isométries (Composée de rotation) 15-05-21 à 17:50

Bonjour ,

3-a)
*Soit \vec{u} et \vec{GH} les vecteurs directeurs unitaires de (D1) et (GH).

Ainsi Mes(\vec{GH} ;\vec{u})=2×\dfrac{2\pi}{3}=\dfrac{4\pi}{3} c'est-à-dire (D_1})=(GH') / H'=R\left(G ;\dfrac{4\pi}{3}\right)(H).

*Soit \vec{v} et \vec{GH} les vecteurs directeurs unitaires de (D1) et (GH).

Ainsi Mes(\vec{GH} ;\vec{v})=-2×\dfrac{2\pi}{3}=-\dfrac{4\pi}{3} c'est-à-dire (D_2})=(HG') / G'=R\left(H;-\dfrac{4\pi}{3}\right)(G).

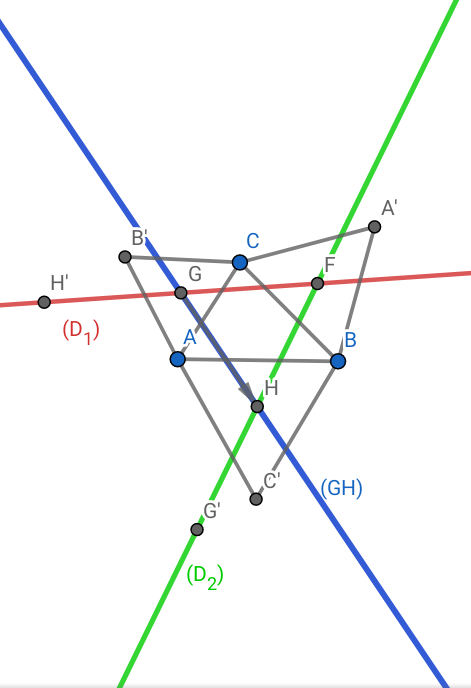
Isométries (Composée de rotation)

Posté par
lakere : Isométries (Composée de rotation) 15-05-21 à 19:57

Bonjour,

  On te demande de "construire". De mon point vue (certainement discutable), une figure suffit.
J'avais préparé celle-ci :

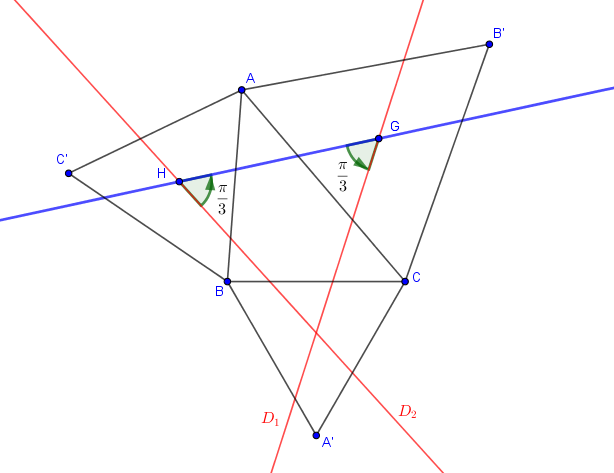
Isométries (Composée de rotation)

Elle parait semblable à la tienne

Note tout de même que je n'ai pas fait apparaître le point F .
C'est l'objet de la question suivante.

Posté par
matheux14re : Isométries (Composée de rotation) 15-05-21 à 20:16

OK

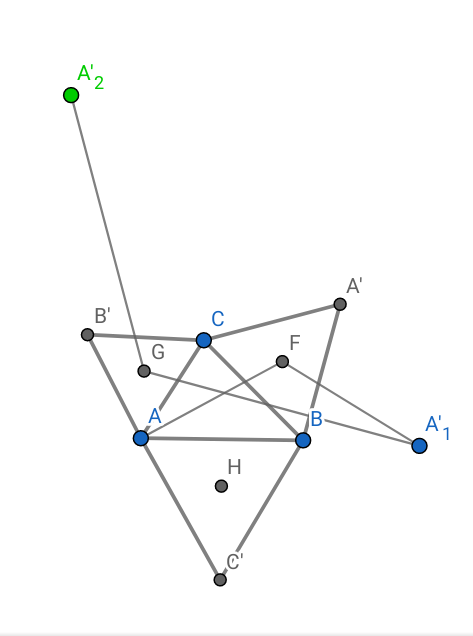
D'après le programme de construction à la question 3-a) , (D_1})=(GH') et (D_2})=(HG').

On en déduit que (D1) et (D2) se coupent au point F.

Posté par
matheux14re : Isométries (Composée de rotation) 15-05-21 à 20:21

D'après les définitions des points H' et G'.

Posté par
lakere : Isométries (Composée de rotation) 15-05-21 à 20:29

Je ne dis pas que c'est faux vu que tu as défini les points G' et H' (je ne dis pas que c'est juste non plus).

Je te propose  autre chose :

D'une part :

  

Citation :
2)d) Du coup, r_2\circ r_3=r_1^{-1} c'est à dire la rotation de centre {\red F} et d'angle -\dfrac{2\pi}{3}


D'autre part :

  r_2\circ r_3=S_{D_1}\circ S_{GH}\circ S_{GH}\circ S_{D_2} d'après la question précédente.
  
  r_2\circ r_3=S_{D_1}\circ S_{D_2}

L'ensemble prouve que D_1 et D_2 se coupent en F.

Qu'en penses-tu ?
  

Posté par
matheux14re : Isométries (Composée de rotation) 15-05-21 à 21:26

Ouais , c'est plus direct comme çà.

La dernière question maintenant.

Posté par
lakere : Isométries (Composée de rotation) 15-05-21 à 21:42

On peut par exemple regarder ma dernière figure en y ajoutant le point F=D_1\cap D_2 (légitime maintenant).

Posté par
matheux14re : Isométries (Composée de rotation) 16-05-21 à 10:07

Oui mais comment cela nous aide à déduire que le triangle GHF est équilatéral direct ?

Posté par
lakere : Isométries (Composée de rotation) 16-05-21 à 12:56

Tout der même : un triangle FGH direct avec deux angles de \dfrac{\pi}{3}.

Posté par
matheux14re : Isométries (Composée de rotation) 16-05-21 à 13:31

L'autre angle vaut π/3 aussi

Merci

Posté par
lakere : Isométries (Composée de rotation) 16-05-21 à 13:34

Posté par
lakere : Isométries (Composée de rotation) 16-05-21 à 14:26

A titre d'exercice, tu peux reprendre ce théorème avec les complexes (A,B,C d'affixes a,b,c dans un certain repère) pour démontrer que FGH est équilatéral.
Cerise que le gâteau, tu montreras en passant que ABC et FGH ont même centre de gravité.

Si on s'y prend "bien", c'est très rapide. Mais malheur à nous si on s'y prend "mal".

Posté par
matheux14re : Isométries (Composée de rotation) 16-05-21 à 14:39

Interressant mais je ne comprends pas vraiment..

Posté par
lakere : Isométries (Composée de rotation) 16-05-21 à 14:47

>> matheux14,

Je vais me permettre de poster une solution "toute faite" relative à cette question (qui n'est pas immédiate si on s'y prend de la mauvaise manière). J'espère ne pas contrevenir à la charte dans ces conditions un peu particulières.
Ceci dit, il faut que je consulte mes "archives" . Cela va prendre un peu de temps...
Pour toi, il est certain que mon prochain message sera "instructif".
N'hésite pas à revenir un peu plus tard

Posté par
matheux14re : Isométries (Composée de rotation) 16-05-21 à 14:56

OK lake

Posté par
mathafou Moderateurre : Isométries (Composée de rotation) 16-05-21 à 15:24

Bonjour,

"tu montreras en passant que ABC et FGH ont même centre de gravité."
et que A'B'C' tant qu'à faire ...

et puis pour compléter le "théorème de Napoléon", qui était le but inavoué de cet exercice (autre que simplement s'entrainer aux compositions d'isométries ) :
"les centres des trois triangles équilatéraux de même orientation érigés sur les côtés de tout triangle ABC forment eux même un triangle équilatéral")

par le point de Napoléon :
que (AF), (BG) et (CH) sont concourantes
par définition en le point appelé "point de Napoléon", X(17) dans l'encyclopédie des centres ETC

On peut le tracer directement dans Geogebra par la commande (peu connue ... )
TriangleCentre( A, B, C, 17 )
de même que l'orthocentre s'obtient directement par
TriangleCentre( A, B, C, 4 )
car l'orthocentre est X(4) dans cette encyclopédie
etc

avec toutes ces autres propriétés de la figure (il y en a encore d'autres), on s'éloigne pas mal de l'exo , même si tout ça est intéressant ...

Posté par
lakere : Isométries (Composée de rotation) 16-05-21 à 23:21

Bonsoir à tous,

La paternité du petit Caporal quant à ce théorème est sujette à caution

Les affixes sont en minuscules. Leurs images sont les points correspondants en majuscules.
A,B,C ont pour affixes a,b,c dans un repère du plan complexe.

Isométries (Composée de rotation)

On utilise l'écriture complexe d'une rotation r de centre \Omega et d'angle \theta :

   M'=r(M)\Longleftrightarrow m'-\omega=e^{i\theta}(m-\omega)
Pour plus de commodité, je note u=e^{i\frac{\pi}{3}}

Par hypothèse :

I\begin{cases}a'=u(b-c)+c\\b'=u(c-a)+a\\c'=u(a-b)+b\end{cases}    et   II\begin{cases}f=\dfrac{a'+c+b}{3}\\\\g=\dfrac{b'+a+c}{3}\\\\h=\dfrac{c'+b+a}{3}\end{cases}

\begin{cases}I\Longrightarrow a'+b'+c'=a+b+c\\II\Longrightarrow f+g+h=\dfrac{a'+b'+c'+2(a+b+c)}{3}\end{cases}

On en déduit : a+b+c=a'+b'+c'=f+g+h

Ce qui signifie que ABC, A'B'C' et FGH ont même centre de gravité (ici noté O)

----------------------------

Par hypothèse :

  III\begin{cases}a-c=u(b'-c)\\b-a'=u(c-a')\\c'-b=u(a-b)\end{cases}

De II on déduit :

  IV\begin{cases}3(g-f)=b'-c+c-a'+a-b\\3(h-f)=a-c+b-a'+c'-b\end{cases} \\     On ne simplifie pas.

de III et IV on déduit :

  h-f=u(g-f)

  FGH est équilatéral direct.

Posté par
matheux14re : Isométries (Composée de rotation) 17-05-21 à 00:01

bn

Merci lake

Posté par
mathafou Moderateurre : Isométries (Composée de rotation) 17-05-21 à 08:35

de façon générale, il ne s'agit pas de la paternité d'un théorème mais du nom qu'on lui donne

Posté par
lakere : Isométries (Composée de rotation) 17-05-21 à 16:29

Bonjour,

Juste pour signaler ceci (j'adhère totalement)

Citation :
elhor_abdelali @ 12-05-2021 à 20:09



je pense qu'il est toujours instructif de retrouver un même résultat mathématique de plusieurs manières.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1674 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !