Inscription / Connexion Nouveau Sujet
Isométries : composée de symétrie glissée et de rotation.
Bonjour ,
Merci d'avance. 
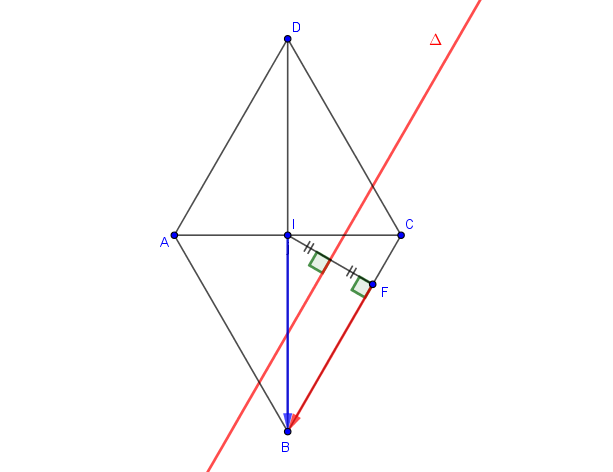
Soit ABCD un losange de sens direct , de centre tel que
.
E est le point tel que et F le projeté orthogonal de
sur (BC).
1) Soit la symétrie glissé d'axe (BD) et de vecteur .
a) Déterminer les images des points A, B et I par s.
b) Préciser la nature et les éléments caractéristiques de s-1.
2) Soit f la transformation du plan définie par f = ros-1 où r est la rotation de centre B et d'angle de mesure .
a) Démontre que
b) Déterminer la nature et les éléments caractéristiques de f.
Réponses
1)
a) *
car
et
.
==> IBCE est un parallélogramme.
*
* car I est le milieu de [BD].
b)
* s-1 est une symétrie glissée d'axe (BD) et de vecteur .
ou == > ne sont pas toujours approprié.
Bonjour à tous,
Juste un petit commentaire:
b)
Tu as de la chance, il y a commutativité mais c'est l'exception.
a) Démontre que
Une erreur ? Plutôt
Je continue donc :
2)a)
tu peux décomposer en un produit de deux symétrie axiales.
à toi de bien les choisir.
Et j'insiste sur le deux points relevés à 12h01 :
1) qui est en général différent de
2) Tu as une erreur d'énoncé en 2)a)
Bon, désolé, j'avais loupé ceci :
et F le projeté orthogonal de
Donc tout va bien
Une remarque après la bataille :
D'après 1), on a s(A) = E ,
s(B) = I
et
s(I) = D .
D'où s-1(E) = A ,
s-1(I) = B
et
s-1(D) =I .
Puis ros-1(E) = r(A) ,
ros-1(I) = r(B)
et
ros-1(D) = r(I) .
Or r(A) = C
et
r(B) = B .
On en déduit f(E) = C
et f(I) = B .
Avec ces deux images, il était clair que l'énoncé de 2) était faux.
Annuler
connectez vous