Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Géometrie plane et dans l'espaceTopics traitant de Géometrie plane et dans l'espace [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Isométries : rotation.

Posté par
matheux14 15-04-21 à 09:15

Bonjour ,

Merci d'avance.

ABC est un triangle équilatéral de sens direct et de centre O.

On considère les points I , J et K les milieux respectifs de [BC] , [AC] et [AB] .

On pose : f=r_{\left(B; \frac{2\pi}{3} \right) }\circ r_{\left(C; \frac{2\pi}{3} \right)}.

a) Déterminer les droites ()1 et ()2 telles que : r_{\left(B; \dfrac{2\pi}{3} \right)}=S_{(\Delta)_{2}} \circ S_{(BC)} et  r_{\left(C ; \dfrac{2\pi}{3} \right)}=S_{(BC)} \circ S_{(\Delta)_{1}} .

b) En déduire la nature et les éléments caractéristiques de f.

Réponses

a) * r_\left(B; \dfrac{2\pi}{3} \right)=S_{(\Delta)_{2}} \circ S_{(BC)}

==> (\Delta)_{2}=]r_\left(B; -\dfrac{\pi}{3} \right)[(BC)]

* r_\left(C; \dfrac{2\pi}{3} \right)=S_{(\Delta)_{BC}} \circ S_{(\Delta)_{1}}

==> (\Delta)_{1}=]r_\left(B; \dfrac{\pi}{3} \right)[(BC)]

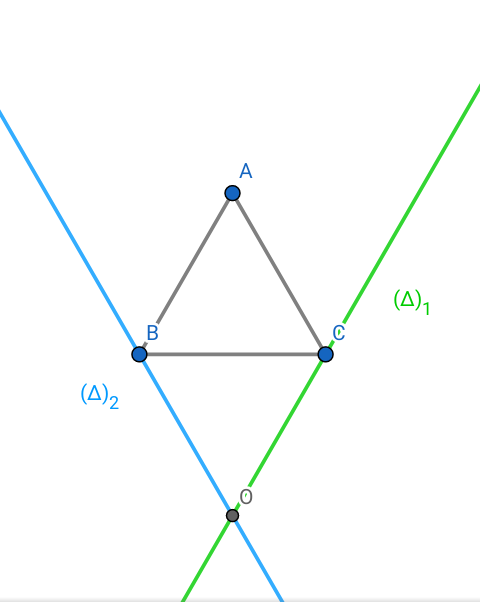
Isométries : rotation.

2) Les droites (?1) et (?2) se coupent au point O et les vecteurs BO et CO sont des vecteurs directeurs des droites (?1) et (?2).

==> f=r_{\left(B; \dfrac{2\pi}{3} \right)} \circ r_{\left(C; \dfrac{2\pi}{3} \right)} =[S_{(\Delta)_{2}} \circ S_{(BC)}] \circ [S_{(\Delta)_{2}} \circ S_{(BC)} ]=r_{\left(O ; 2×\dfrac{2\pi}{3} \right)}=r_{\left(O ; \dfrac{4\pi}{3} \right)}

Posté par
malou Webmasterre : Isométries : rotation. 15-04-21 à 09:45

re
j'ai l'impression que tu as la même erreur que dans ton autre exercice
tu composes tes applications à l'envers
quand tu écris S_{(\Delta)_{2}} \circ S_{(BC)} tu dois commencer par S(BC) et toi tu fais le contraire si je lis bien
donc à reprendre

Posté par
mathafou Moderateurre : Isométries : rotation. 15-04-21 à 11:20

Bonjour à vous deux,

et puis (à propos de ta figure)
l'énoncé dit : un triangle ABC et son centre O

si tu crées un autre point ailleurs, tu dois l'appeler autrement que "O" !
le point que tu as baptisé O n'est certainement pas le centre du triangle équilatéral !
(I, J et K sont aussi des noms deja pris)

Posté par
matheux14re : Isométries : rotation. 16-04-21 à 00:03

a) * r_\left(B; \dfrac{2\pi}{3} \right)=S_{(\Delta)_{2}} \circ S_{(BC)}

==> (\Delta)_{2}=r_\left(B; \dfrac{\pi}{3} \right)[(BC)]=(AB)

* r_\left(C; \dfrac{2\pi}{3} \right)=S_{BC} \circ S_{(\Delta)_{1}}

==> (\Delta)_{1}=r_\left(B; -\dfrac{\pi}{3} \right)[(BC)]=(AC)

2) Pas vraiment convaincu que je dois faire comme dans mon premier poste..

Posté par
malou Webmasterre : Isométries : rotation. 16-04-21 à 09:01

oui, et maintenant tu utilises ça (simplifie l'écriture de f obtenue), pour faire la question suivante qui va être immédiate

Posté par
matheux14re : Isométries : rotation. 16-04-21 à 15:40

\large{f=r_{\left(B; \frac{2\pi}{3} \right) }\circ r_{\left(C; \frac{2\pi}{3} \right)}}=[S_{(\Delta)_{2}} \circ S_{(BC)} ]\circ [S_{(BC)} \circ S_{(\Delta)_{1}}]

Posté par
malou Webmasterre : Isométries : rotation. 16-04-21 à 15:45

matheux14 @ 16-04-2021 à 15:40

\large{f=r_{\left(B; \frac{2\pi}{3} \right) }\circ r_{\left(C; \frac{2\pi}{3} \right)}}=[S_{(\Delta)_{2}} \circ {\underbrace{S_{(BC)} ]\circ [S_{(BC)} }\circ S_{(\Delta)_{1}}]


allez....que vaut ce que j'ai mis ensemble ?

Posté par
matheux14re : Isométries : rotation. 16-04-21 à 16:04

C'est l'identité du plan.

Donc f= S_{(\Delta_{2})} \circ S_{(\Delta_{1})}=r\left(A ; \dfrac{2\pi}{3}\right)

Car d'après la question précédente , (\Delta_{1})=(AC) et (\Delta_{2})=(AB)  et ABC est un triangle équilatéral direct :

Mes(\vec{AB} ; \vec{AC})=\dfrac{\pi}{3}.

Posté par
malou Webmasterre : Isométries : rotation. 16-04-21 à 16:32

donc tu arrives à

f= S_{(AB)} \circ S_{(AC)}

il vaut mieux les appeler par leurs noms, c'est plus facile

mais cela ne fait pas ce que tu dis au niveau angle

Posté par
matheux14re : Isométries : rotation. 16-04-21 à 17:39

Donc f= S_{(\Delta_{2})} \circ S_{(\Delta_{1})}=r\left(A ; -\dfrac{2\pi}{3}\right)

Car d'après la question précédente , (\Delta_{1})=(AC) et (\Delta_{2})=(AB)  et ABC est un triangle équilatéral direct :

Mes(\vec{AC} ; \vec{AB})=-\dfrac{2\pi}{3}.

Donc f= S_{(AB)} \circ S_{(AC)}=r\left(A ; -\dfrac{2\pi}{3}\right).

Posté par
malou Webmasterre : Isométries : rotation. 16-04-21 à 17:50

oui, voilà

Posté par
matheux14re : Isométries : rotation. 16-04-21 à 17:52

Merci

Posté par
mathafou Moderateurre : Isométries : rotation. 16-04-21 à 18:19

une petite erreur (de frappe ?)

Mes(\vec{AC} ; \vec{AB})={\red-\dfrac{\pi}{3}} (pas -2pi/3)

et l'angle de la rotation est {\red 2}Mes(\vec{AC} ; \vec{AB}) = -\dfrac{2\pi}{3}

Posté par
matheux14re : Isométries : rotation. 16-04-21 à 18:32

Désolé , c'est une erreur de frappe..

Merci.

Posté par
malou Webmasterre : Isométries : rotation. 16-04-21 à 18:43

oui, en lisant en "diagonale", je ne l'avais pas vue
Bonne soirée


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1674 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !