Inscription / Connexion Nouveau Sujet
J'ai un problème avec un exercice de maths:
bonjour :
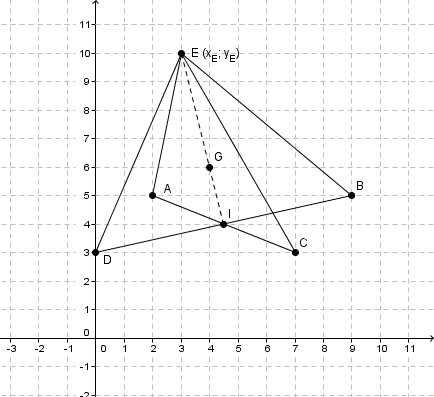
Dans le plan muni d'un repère (O,I,J),on considère les points A(2;5),B(9;5),C(7;3) et
D tel que [AC] et [BD] aient le même milieu. Le point G est le centre de gravité du
triangle AEC.
1-Dans cette question,E (3;-5) Montrer que G est aussi le centre de gravité du triangle BDE. On pourra admettre que le point G est le centre de gravité du triangle
MNP si et seulement si: vecteur GM+vecteur GN+vecteurGP=vecteur0.
2-Désormais, E est un point quelconque du plan.On note ses coordonnées.Montrer
que le résultat de la question précédente se généralise.
J'ai résolu la première question en prouvant que vec GE+vec GD+vec GB=vec 0.
Mais je ne sais comment m'y prendre pour la deuxième question.
quelqu'un peut il m'aider SVP ?[/u][/i][/b]
bonsoir,
2)pose E(xE ; yE) et G(xG ; yG)
puisque G est centre de gravité du triangle AEC, on a (en vecteurs) GA + GE + GC = 0
exprime les coordonnées de GA, de GE et de GC,
et tu obtiens xE + 9 - 3xG = 0
et yE + 8 - 3yG = 0
ensuite,
exprime les coordonnées des vecteurs GE, GD et GB
calcule GE + GD + GB .. peux tu dire que c'est egal au vecteur nul ?
si oui, G est aussi centre de gravité de BDE.. et tu as généralisé !
bonjour,
est ce que tu as relu ton cours ?
tu ne "comprendras" pas si tu ne maîtrises pas le cours. C'est un minimum.
tu dis que tu as répondu à la question en prouvant que GE+GB+GD = 0
comment as tu fait ?
pose E(xE ; yE) et G(xG ; yG)
exprime les coordonnées des vecteurs GA, GE et GC
vas y !
c'est un ami qui avait posé l'énoncé mais je ne sais pas comment il a fais on a chercher dans mes cours mais il y a rien qui puisse m'aider sinon on aurais pas mit cette exercice en ligne , apres je ne sais pas comment il a fait
Bonjour,
J'ai résolu la première question en prouvant que vec GE+vec GD+vec GB=vec 0.
donc tu as résolu ou bien quelqu'un d'autre a résolu cette question 1 ??
parce que la question 2 c'est exactement les mêmes calculs en remplaçant partout les valeurs numériques des coordonnées de E par "xE" et "yE", ni plus ni moins.
ah !
alors pourquoi prétendre que tu avais fait la question 1 ? ça induit en erreur ceux qui voudraient t'aider !
rappel :
coordonnées d'un vecteur (cours)
si un vecteur a pour origine A (xA; yA) et extrémité B (xB; yB) , ses coordonnées sont (xB-xA; yB-yA)
le vecteur nul a pour coordonnées (0; 0)
somme de vecteurs à partir de leurs coordonnées (idem, cours) :
si on a  = (a; b) et
= (a; b) et  = (c; d)
= (c; d)
alors  +
+ a pour cooronnées (a+c; b+d)
a pour cooronnées (a+c; b+d)
reste donc à voir ce que veut dire la définition de "centre de gravité" avec cet aspect vecteurs
et donc de calculer dès le départ les coordonnées du point G.
appelons les x et y puisque pour l'instant on ne les connait pas
G centre de gravité de AEC veut dire de par la définition que GA + GE + GC = 0 (tout en vecteur)
GA a pour coordonnées (xA - x; yA - y) c'est à dire (2-x; 5-y)
pareil pour les autres et écrire que la somme = 0 te donne
d'une part une équation en x : (2-x) + (...) + (...) = 0 à résoudre
d'autre part une équation en y idem.
ensuite la question 1 consiste à vérifier que cette condition GE+GB+GD = 0 est alors vraie avec ces coordonnées de G qu'on vient de calculer.
et la question 2 est exactement pareil, sauf que E n'a pas pour coordonnées (3;-5) mais ce qui est marqué dans ton énoncé que tu n'as pas recopié correctement ici :
On note ses coordonnées
copier coller une image ne marche pas.
utilises donc des caractères ordinaires à la place ici (a, x, va savoir, à toi de choisir)
tu peux aussi mettre des
 ,
,  etc que tu trouves dans la barre de symboles affichée par le bouton
etc que tu trouves dans la barre de symboles affichée par le bouton  (juste cliquer sur le symbole, ne pas chercher à le "copier-coller" ou à le "glisser-déposer", simple clic dessus)
(juste cliquer sur le symbole, ne pas chercher à le "copier-coller" ou à le "glisser-déposer", simple clic dessus)je rappel que c'est mon ami qui a posté cette énoncé
je sais que
1) cherche les coordonnées de D
2) cherche les coordonnées de G
3) vérifie que vecGB + vecGD + vecGE = 0
4) Fais de même mais avec E(xE ; yE)
mais le problème et que je ne sais pas comment faire enfin comment le marqué
1) chercher les coordonnées de D :
rappel de cours : savoir parfaitement son cours est tout ce qui est demandé dans cet exo.
mais c'est absolument indispensable de réviser le cours avant de faire les exos.
si P(xP; yP) et Q(xQ; yQ) alors le milieu de PQ a pour coordonnées
utiliser cette propriété pour :
calculer le milieu de AC
chercher les coordonnées (xD; yD) de D pour que le milieu de BD soit le même que le point qu'on vient de calculer.
les points 2 et suivants de ton dernier post c'est ce que j'avais dit avant.
fais le (je t'ai donné bien plus de détails que le "plan" que tu cites)
tu parles de quelle question là ???
fais donc tout dans l'ordre, pas en jetant une formule qui n'arrivera que au bout de 10 lignes de calculs préalables (coordonnées de D etc ...)
vu que tu es coincée sur la question 1, et il n'y a pas de xE, yE dans cette question 1
fais la donc déjà pour commencer cette question 1
sinon ça n'a aucun sens.
pour moi tu étais coincée à
1) cherche les coordonnées de D
c'est toi qui les as trouvées ou c'est tes potes ??
tu as compris ce que je t'ai écrit ici :
somme de vecteurs à partir de leurs coordonnées (idem, cours) :
si on a
 = (a; b) et
= (a; b) et  = (c; d)
= (c; d)
alors
 +
+ a pour coordonnées (a+c; b+d)
a pour coordonnées (a+c; b+d)faire du n'importe quoi ainsi (je sais faire je sais pas faire, je crache un truc et puis non je sais saispas faire, et que je te mélange les questions etc.)
va juste décourager qui que ce soit de t'aider.
Je suis aussi bloqué sur cette exercice #mathafou si tu peux m'aider stpp je suis aussi bloquer sur la 1ere j'ai fais ce que ta demander un peu plus haut c'est a dire résoudre les équations avec x et y mais maintenant je sais plus quoi faire..
Bonjour,
J'ai exactement le même problème a effectuer.
J'aurais besoin d'aide pour la question 2.
Quelqu'un pourrait-il m'aider s'il-vous-plaît ? 
Voilà ce que j'ai fait :
(Je sais donc que D = (0;3) et que G = (4;1) (grâce à l'exo 1)
J'ai donc remplacé les coordonnées de E par (xE;yE)
J'ai calculé les coordonnées des vecteurs GB, GD et GE :
GB = 9 - 4 ; 5 - 1
= (5 ; 4)
GD = 0 - 4 ; 3 - 1
= (-4 ; 2)
GE = xE - 4 ; yE - 1
= (xE - 4 ; yE - 6)
Puis j'ai effectué l'opération : GB + GD + GE = 0
x : 5 - 4 + xE - 4 = -3 + xE
y : 4 + 2 + yE - 1 = 5 +yE
J'aurais besoin d'éclaircissement merci d'avance 
J'ai d'ailleurs oublié de préciser que dans l'énoncé de l'exo 2, il n'y a rien après "On note ses coordonnées".
Je pense que cela signifie que pour tous E (xE ; yE), il faut montrer que GB + GD + GE = 0 
Bonjour,
dans la question 2, G n'a pas du tout les coordonnées (4; 1) mais à des coordonnées qui dépendent de celles de E
il faut en fait tout refaire à partir du début avec (xE; yE) comme coordonnées de E, écrites xE et yE
Bonjour et merci de votre réponse 
Je n'ai pas vraiment compris comment je dois utiliser G,
GB = 9 -xG ; 5 - yG
GD = 0 - xG ; 3 - yG
GE = xE - xG; yE - yG

Ou dois-je essayer de trouver des égalités entre vecteurs ?
exactement comme tu as fait pour la question 1)
à moins que tu ne l'aies pas vraiment faite ??
question 1 :
en vecteur GA + GC + GE = 0 car G est le centre de gravité de ACE par définition.
se traduit sur les abscisses :
(xA - xG) + (xC - xG) + (xE - xG) = 0
question 1 on connait xE :
2 - xG + 7 - xG + 3 - xG = 0
3xG = 2 + 7 + 3 = 12
xG = 4
etc
dans la question 2) exactement les mêmes calculs mais avec xE écrit xE :
2 - xG + 7 - xG + [rouge]xE[/rouge] - xG = 0
...
xG = une fonction de xE
etc.
Je me suis cassée la tête à tout faire moi-même alors dites pas que je l'ai pas fait s'il vous plaît 
Pour la question 1, j'avais directement commencé avec GB + GD + GE = 0
Donc ACE :
GA + GC + GE = 0
GA = 2 - xG
5 - yG
GC = 7 - xG
3 - yG
GE = xE - xG
yE - yG
x : 2 - xG + 7 - xG + xE - xG = 0
-3xG + xE = -9
y : 5 - yG + 3 - yG + yE - yG = 0
-3yG + yE = -8
On doit donc chercher la valeur de G en fonction de E (désolée j'avais pas compris  )
)
x : 2 - xG + 7 - xG + xE - xG = 0
-3xG + xE = -9
xG + xE = 9/3
xG = 3 - xE
y : 5 - yG + 3 - yG + yE - yG = 0
-3yG + yE = -8
yG + yE = 8/3
yG = 8/3 - yE
Et si j'ai a peu près compris :
GA = 2 - 3 - xE
5 - 8/3 - yE
= (-1 - xE ; 7/3 - yE)
GC = 7 - 3 - xE
3 - 8/3 - yE
= (4 - xE ; 1/3 - xE)
GE = xE - 3 - xE
= yE - 8/3 - yE
= (-3 ; -8/3)
Pour finir :
x : -1 - xE + 4 - xE - 3 = 0
-2xE = 0
xE = 0
y : 7/3 - yE + 1/3 - yE - 8/3 = 0
-2yE = 0
yE = 0
Pouvez-vous me dire si j'ai bon ou pas s'il vous plaît (je pense que j'ai bon  )
)
désolé je n'avais pas compris ce que tu n'avais pas compris.
tu fais des erreurs de calcul
-3xG + xE = -9
xG + xE = 9/3 faux
on ne "fait pas passer" n'importe quoi n'importe comment
en fait "faire passer" est une opération qui n'existe pas
c'est un raccourci de langage
la vraie opération est :
je divise les deux membres par 3 (ou ici par -3 si tu préfères), en détail :
(-3xG + xE)/(-3) = (-9)/(-3) je divise les deux membres par -3, je fais de façon générale la même chose des deux côtés pour que ça reste égal
(-3xG)/(-3) + xE/(-3) = (-9)/(-3) distribution
xG - xE/3 = 3 simplification
etc (pareil partout)
J'ai un problème : 
Je n'arrive pas à trouver un moyen de plus simplifier
xG - xE/3 = 3
Dois-je passer xE du côté du trois et dois-je faire :
xG*3 - (xE/3)*3 = 3*3
3xG = 9 -xE
?
encore un "faire passer" foireux ??
faudrait revoir les bases du calcul (début collège), ou alors très grosse fatigue ??
A - B = C
donne A = C + B en ajoutant B aux deux membres :
(A-B)+B = C + B
A - B + B = C + B
A = C + B
Sûrement les deux. De plus, notre prof nous avait appris à faire directement. Il disait qu'il fallait juste changer de signe:
A - B = C
A = C+B
J'ai réessayer :
xG - xE/3 = 3
-xG + xG - xE/3 = 3 -xG
xE/3 = 3 - xG
des fatras.
avec ta règle (source d'innombrables erreurs, la preuve !!!) de "faire passer en changeant de signe"
xG - xE/3 = 3
qu'est ce qu'on cherche ?? c'est xG qu'on cherche
donc le reste je le "fais passer" de l'autre côte ("en changeant de signe" ce que je "fais passer", pas je ne sais quoi d'autre  )
)
xG = 3 + xE/3
terminé
(et pareil pour tous les autres)
J'ai encore réessayé :
xG + xE/3 = 3
xG + (xE/3)*3 = 3*3
xG + xE = 9
xG + xE - xE = 9 - xE
xG = 9 - xE
encore plus de fatras faux et farfelu dû à des "faire passer" de n'importe quoi n'importe comment n'importe où ...
no comment.
le premier membre forme UN TOUT, pas des petits bouts
si je multiplie par 3 je multiplie TOUT, pas seulement un petit bout etc
et c'est loufoque de multiplier par 3 alors que justement on venait de diviser par 3 
J'ai à présent réessayé pour y :
-3yG + yE = -8
-3yG/-3 + yE/-3 = -8/-3
yG - yE/3 = 8/3
yG = 8/3 + yE/-3
?
Est-ce différent entre les multiplications et les divisions, et les additions et les soustractions ? 
Car vous dites "si je multiplie par 3 je multiplie TOUT"
Mais pour les additions et les soustractions, on n'ajoute pas à tous les membres :
(A-B)+B = C + B
A - B + B = C + B
A = C + B
encore des changements de signe loufoques ...
-yE/3 quand on le change de signe ne donne pas yE/-3
yE/-3 = -yE/3 et c'est faux ça n'a pas changé de signe
-yE/3 changé de signe ça fait +yE/3
encore une fois ces histoires de changement de signe te mettront plusieurs années à être maitrisées correctement
cette méthode de recette de cuisine est dangereuse
elle ne devrait être enseignée que une fois qu'on maitrise parfaitement ce qu'on fait vraiment
à savoir :
faire la même chose des deux côtés du signe "=" et rien d'autre
ici j'ajoute yE/3 des deux côtés, de sorte que le "-yE/3" qui est à gauche "disparaisse"
et qu'on a l'impression qu'on a fait par un tour de passe-passe "passer" ce terme de gauche à droite en changeant son signe
les maths c'est pas des tours de passe-passe ni des recettes de cuisine.
PS ton deuxième message
revoir les bases des bases en 5ème sur les opérations en général
et le vocabulaire :
____ tout ça c'est le 1er membre de l'égalité
/ \
A + B = C
| | \__/ et tout ça c'est le second membre de l'égalité
| |
| un autre terme du même 1er membre
un terme du 1er membre
A - B = C
(A-B)+B = C + B
j'ai bien ajouté B à A-B qui forme un tout, c'est pour ça que je l'ai mis entre parenthèses ce "A-B" pour bien montrer que c'est un tout, tout ce qui était au premier membre, au membre de gauche.
avec une multiplication on aurait par exemple
A-B = C/3
je multiplie par 3
(A-B)×3 = (C/3)×3 là aussi le "A-B" forme un tout et je le mets entre parenthèses pour bien monter que c'est un tout
ensuite pour supprimer les parenthèses voir le cours de 5ème.
(A+B)-B = A + B - B règle de 5ème sur la suppression des parenthèses
et (A-B)×3 = A×3 - B×3 = 3A - 3B autre règle de 5ème toujours sur la suppression des parenthèses avec une multiplication (= "distribution")
en seconde tout ceci ne devrait absolument pas nécessiter de telles explications !!!! (ni de détailler autant toutes ces étapes)
c'est vu, revu et rerevu depuis la 5ème ! et déja pratiqué depuis plusieurs années donc.
les calculs devraient être faits directement du premier coup sans autant d'erreurs !!
tu n'y arriveras pas si à chaque petite opération tu es obligé de faire autant d'efforts pour obtenir finalement des trucs faux .
salut
ou une autre facon de repondre à la question :Montrer que G est aussi le centre de gravité du triangle BDE
on a comme données:
a.GA + e.GE + .cGC = 0 ---> (a+e+c).G = A + E + C
IA + IC =0 ---> 2I = A + C
IB + ID = 0 ---> 2I = B+ D I milieu de AC et aussi de BD
alors (a+e+c).G = A + E + C = B + D + E.
on a donc (a+e+c).G = B + D + E .
soit en passant par G : (a+e+c).GG = GB + GD + GE = 0
d'ou GB+ GD + GE = 0 et donc G,3 est barycentre de B,1 D,1 et E,1
pas dit que en seconde l'addition de points soit définie !!
et puis c'est quoi ces "a, b, c" ??? pour moi c'est 1 partout ! l'énoncé dit GA + GC + GE = 0, pas des trucs en plus.
autre façon aussi court-circuitant l'exo :
soit I le milieu commun de AC et BD
alors G est au tiers de EI à partir de I dans ACE (propriété de collège)
mais le centre de gravité de BDE est lui aussi au 1/3 de EI à partir de I
terminé en deux lignes, et ce quelles que soient les coordonnées de quoi que ce soit.
mais ce n'est pas ce que demande l'énoncé avec des coordonnées de points etc.
Rebonjour,
Je crois que j'ai enfin compris comment faire les calculs (j'ai même rêvé d'équations cette nuit lol).
Donc :
Triangle ACE
GA+GC+GE = 0
GA : 2 - xG
5 - yG
GC : 7 - xG
3 - yG
GE : xE - xG
yE - yG
x : 2 - xG + 7 - xG + xE - xG = 0
-3xG + xE = -9
(-3xG+xE)*(-1/3) = -9*(-1/3)
-3xG*(-1/3) + xE*(-1/3) = -9*(-1/3)
xG - xE/3 = 3
xG = 3 + xE/3
y : 5 - yG +3 - yG + yE - yG = 0
-3yG + yE = -8
(-3yG+yE)*(-1/3) = -8*(-1/3)
-3yG*(-1/3) + yE*(-1/3) = -8*(-1/3)
yG - yE/3 = 8/3
yG = 8/3 + yE/3
(Suite)
GA : -2 - 3 +(xE/3) ---> ((-5+(xE/3) ; (7/3)+(yE/3))
5 - (8/3) + (yE/3)
GC : 7 - 3 +(xE/3) ---> ((4+(xE/3) ; (1/3) + (yE/3))
3 - (8/3) + (yE/3)
GE : xE - 3 +(xE/3) ---> ((-3 + (4xE/3) ; (-8/3)+(4yE/3))
yE - (8/3) + (yE/3)
x : -5 + (xE/3) + 4 + (xE/3) - 3 + (4xE/3) = 0
6xE/3 = 4
(3/6)*(6xE/3) = 4*(3/6)
xE = 12/6
xE = 2
y : (7/3) + (yE/3) + (1/3) + (yE/3) - (8/3) + (4yE/3) = 0
(6yE/3) = 0
(3/6)*(6yE/3) = 0*(3/6)
yE = 0
OK pour xG = 3 + xE/3 et yG = 8/3 + yE/3
(Suite) euh pourquoi tu calcules GA, GB et GC ?
pour vérifier que GA+GB+GC =0 ? on le sait déja, c'est ça qui a permis de calculer les coordonnées de G !
ça ne sert qu'à vérifier que tu ne fais pas d'erreurs de calcul et rien d'autre.
ce qu'il faut calculer c'est GB + GD + GE
(pour savoir si oui ou non cette somme est nulle, c'est à dire si oui ou non G est le centre de gravité de BDE
c'est ça qu'on demande)
de toute façon c'était faux ton calcul
GA : -2 - 3 +(xE/3) euh... xA - xG = 2 - (3 + xE/3) = 2 - 3 - xE/3 = -1 - xE/3
etc (tout est pareil)
et tes x, y à la fin devraient être tous les deux nuls (car GA+GC+GE est = 0 par construction de G, quel que soit E)
on ne cherche pas xE, yE, ce n'est pas des équations dont les inconnues seraient xE et yE
xE et yE sont choisies arbitrairement (un point E n'importe où) et s'écrivent xE, yE et c'est tout
obtenir 0 = 0 (ce que tu aurais dû obtenir avec un calcul correct) ne va certes pas déterminer une valeur pour xE et yE !
ne fais pas les mêmes erreurs dans le calcul de GB, GD (et le même GE à refaire correctement)
GB + GD + GE = 0 ?
GB : 9 - xG
5 - yG
GE : xE - xG
yE - yG
GD : 0 - xG
3 - yG
x : 9 - xG + xE - xG + 0 - xG = 0
-3xG + xE = -9
(-1/3)*-3xG + xE*(-1/3) = -9*(-1/3)
xG - (xE/3) = 3
xG = 3 + (xE/3)
y : 5 - yG + yE - yG + 3 - yG = 0
-3xG + xE = -8
(-1/3)*-3yG + yE*(-1/3) = -8*(-1/3)
yG - (yE/3) = 8/3
yG = (8/3) + (yE/3)
GB : 9 - (3+xE/3) ---> (6 - xE/3)
5 - (8/3+yE/3) (7/3 - yE/3)
GE : xE - (3+xE/3) ---> (2xE/3 - 3)
yE - (8/3+yE/3) (2yE/3 - 8/3)
GD : 0 - (3+xE/3) ---> (-3 - xE/3)
3 - (8/3+yE/3) (1/3 - xE/3)
x :
= 6 - xE/3 + 2xE/3 - 3 - 3 - xE/3
= 6 - 6 - 2xE/3 + 2xE/3
= 0
y :
= 7/3 - yE/3 + 2yE/3 - 8/3 + 1/3 - yE/3
= 8/3 - 8/3 - 2yE/3 + 2yE/3
= 0
GB + GD + GE = 0.
J'en conclus que le résultat de la question précédente se généralise avec E étant un point quelconque du plan.
j'ai pas lu tout le détail d'un tel pavé au minimum deux fois trop fouillis pour ce qu'on veut calculer ...
mais comme tu trouves 0, c'est bon.
on veut vérifier que GB + GE + GD = 0
pour cela on calcule uniquement
GB : xB - xG = 9 - (3 + xE/3) = 6 - xE/3
yB - yG = 5 - (8/3 + yE/3) = (15-8)/3 - xE/3 = 7/3 - yE/3
GE : xE - xG = xE - (3 + xE/3) = xE - 3 - xE/3 = 2xE/3 - 3
yE - yG = yE - (8/3 + yE/3) = 2yE/3 - 8/3
GD : xD - xG = 0 - (3 + xE/3) = -3 - xE/3
yD - yG = 3 - (8/3 + yE/3) = 1/3 - yE/3
calculons GB + GE + GD
x = (6 - xE/3) + (2xE/3 - 3) + (-3 - xE/3) = 6 - 3 - 3 + 3xE/3 - xE/3 - xE/3 = 0
y = (7/3 - yE/3) + (2yE/3 - 8/3) + ( 1/3 - yE/3) = 7/3 + 1/3 - 8/3 + 2yE/3 - yE/3 - yE/3 = 0
ce qu'il fallait démontrer et c'est terminé.




