Inscription / Connexion Nouveau Sujet
l'orthocentre d'un triangle
Bonjour,
j'ai un DM à rendre dans quelques jours et ça fait des jours que je suis dessus, en vain. J'ai besoin d'aide s'il vous plaît.
Voici l'intitulé:
Soit ACC un triangle, A', B' et C' les milieux respectifs de [BC], [CA] et [AB], et O le centre du cercle circonscrit au triangle ABC.
1. Faire une figure à la main.
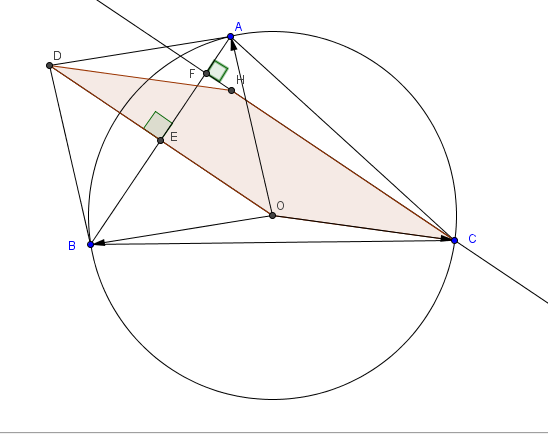
2. a. Construire le point D tel que (vecteur)OD = (vecteur)OA + (vecteur)OB.
Quelle est la nature du quadrilatère OADB ?
b. En déduire que les droites (OD) et (AB) sont perpendiculaires.
3. a. Construire H tel que (vecteur)OH = (vecteur)OA + (vecteur)OB + (vecteur)OC.
b. Quelle est la nature du quadrilatère ODHC ?
c. En déduire que (CH) est perpendiculaire à (AB).
4. Quelles autres relations démontrerait-on de même ? En déduire une propriété des trois hauteurs d'un triangle.
***
ce que j'ai trouvé:
1 le cercle a été fait
2 a OADB est un losange
b parce que OADB est un losange, (CH) et (AB) sont les diagonales du losange et sont donc perpendiculaires en C'
3. JE N'Y ARRIVE PAS! je n'arrive pas à trouver le point H et additionner mes trois vecteurs
je remercie à l'avance tous ceux qui m'aideront
Bonsoir
losange oui
propriété des diagonales d'un losange oui
construction de H en tenant compte de ce qui précède
ce qui devrait vous permettre de construire H
nature de OCHD voir construction de la somme de deux vecteurs
si deux droites sont perpendiculaires toute parallèle à l'une est perpendiculaire à l'autre
refaire la même chose en prenant puis