Inscription / Connexion Nouveau Sujet
L'orthocentre d'un triangle
Bonjour j'ai un DM a faire je voudrais de l'aide svp
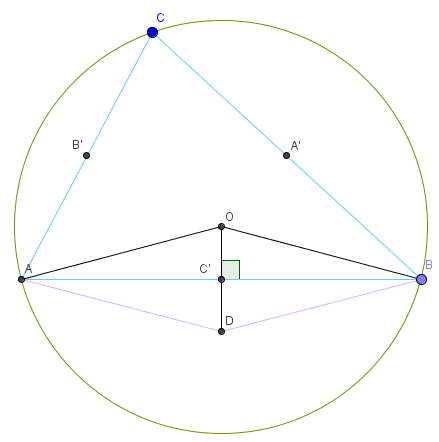
Soit ABC un triangle , A' , B' , C' les milieux respectifs de [BC] , [CA] et [AB] , et O le centre du cercle circonscrit au triangle ABC.
1) Faire une figure à la main ou avec un logiciel.
2) a. Construire le point D tel que vecteur OD = vecteur OA+ vecteur OB.
Quelle est la nature du quadrilatère OADB?
b) en déduire que les deoites(OD)et (AB) sont perpendiculaires.
3)a. Construire H tel que vecteur OH= vecteur OA+ vecteur OB + vecteur OC
b) Quelle est la nature du quadrilatère ODHC?
c)En déduire que (CH) est perpendiculaire à (AB).
4)Quelles autres relations démontrerait-on de même? En déduire une propriété des trois hauteurs d'un triangle.
Merci beaucoup pour la figure au passage très bonne années à vous , par contre les questionsqui se rapporte à l'exercice pouvez- vous m'aider ?
Bonjour
bonne année à vous aussi
D est le quatrième sommet du parallélogramme AOBD
c'est tout simplement la définition de la somme de deux vecteurs
quant à la nature je vous laisse compléter
b Dans un les diagonales sont
3
utilisez la relation de Chasles
peu d'intérêt
parallélogramme par construction
2 côtés consécutifs de même longueur c'est donc un losange
et dans un losange les diagonales sont perpendiculaires
Chasles avait pour prénom Michel
Par contre la figure est complete ? Parcequ'il manque le point H mais je n'est pas compris comme le placer
vous pouvez construire la somme des vecteurs
vous avez pu utiliser la relation de Chasles
vous avez montré que H est un sommet du parallélogramme ODHC
c'était aussi à cela que je répondais
par conséquent CHDO est un
dans un les côtés opposés sont
par conséquent les droites sont
si deux droites sont parallèles, toute perpendiculaire à l'une l'est aussi à l'autre
Donc si je comprend bien : CH= OD par consequent ODCH est un parallélogramme . Dans un parallélogramme les cotes opposés sont parallèle.
C) CH est perpendiculaire a AB car si deux droites sont parallele , toute perpendiculaire a l'une et aussi a l'autre
il faudrait être un peu plus précise
par conséquent CHDO est un parallélogramme
dans un parallélogramme les côtés opposés sont parallèles
par conséquent les droites (CH) et (OD) sont parallèles
si deux droites sont parallèles, toute perpendiculaire à l'une l'est aussi à l'autre
on a montré que (OD) était perpendiculaire à (AB) par conséquent (CH) est perpendiculaire à (AB)
que peut-on dire alors de (CH) ?