Inscription / Connexion Nouveau Sujet
La pyramide du Louvre - Géométrie dans l'espace - 2nde
Bonjour à tous. C'est mon premier post sur ce site, j'espère que certains d'entre vous pourront m'aider, je vous en remercie par avance. 
JE SAIS QUE CE SUJET A DEJA ETE POSTE MAIS JE BLOQUE SUR LA QUESTION 3 QUI IL ME SEMBLE N'A ETE RESOLUE DANS AUCUN TOPIC (JE PEUX ME TROMPER).
J'ai un exercice de géométrie dans l'espace sur la pyramide du Louvre.
Voici les questions de la première partie avec l'énoncé :
" La pyramide du Louvre est une pyramide de verre et de métal située au milieu de la cour Napoléon au musée du Louvre à Paris. Elle s'élève à 21m sur une base carrée de 35m de côté. La pyramide est composée de 603 losanges et 70 triangles en verre. "
1. Dessiner en perspective cavalière la pyramide ABCDE.
2. On veut tracer un patron de la pyramide tel que le côté de la base mesure 10cm. Quelle sera alors la hauteur de la pyramide sur le patron ? Quelle échelle doit on utiliser ?
3. Tracer le triangle AOE puis un patron de la pyramide à l'échelle obtenue à la question 2
4. Calculer le volume de la pyramide en m^3.
Mes réponses :
1. C'est fait.
2. La hauteur sera de 6cm → (2100*10)/3500=6
L'échelle est-elle 3500/10 ??? Je ne suis pas sûre...
3. Je n'arrive pas à faire cette question. Je sais que EO=6cm mais comment trouver les autres côtés du triangle avec des valeurs exactes ? Je n'y arrive vraiment pas. Pythagore et la trigonométrie ne fonctionnent pas. Du coup je ne peux tracer ni le triangle ni le patron... Aidez-moi s'il vous plait !
4. Pas encore fait mais ça je saurai me débrouiller.
Cet exercice est à rendre bientôt, alors s'il vous plaît aidez-moi, je vous en serai vraiment reconnaissante. ^^
Merci beaucoup !
Bonjour ,
l'échelle c'est à l'envers
une échelle > 1 voudrait dire que le modèle est plus grand que l'original !
question 3 :
mais si, Pythagore marche très bien
tu coupes par un plan vertical passant sur la diagonale de la base
tu dois voir aparaitre un triangle rectangle qui te permet de calculer par Pythagore l'arête à partir de la hauteur (connue) et de la demi diagonale de la base (facile, un autre Pythagore au besoin mais la diagonale d'un carré c'est "du connu") .
sinon on peut faire ça "par construction" sans rien calculer du tout
c'est à dire en construisant le triangle rectangle précédent et en reportant son hypoténuse en tant qu'arètes de la pyramide.
Merci beaucoup de m'aider.
Ah oui, pour l'échelle, c'est bien le fait que ce soit >1 qui me dérangeait.
Du coup le triangle rectangle qui apparait a pour hauteur 6 cm, un côté qui est une arête de la pyramide et le dernier côté est une demi diagonale de la base.
La diagonale de la base ABCD s'appelle AC. La base carrée a des coôtés de 10cm.
On applique Pythagore :
AC²= AB²+BC²
= 10²+10²= 100+100=200
Donc AC=√ 200 mais du coup ça ne me fait pas de valeur exacte.
Et pour trouver la valeur AO qui est celle de la demi-diagonale de dois faire √ 200/2 et ça n'est pas non plus une valeur exacte...
Je n'ai peut-être pas bien compris ce que vous vouliez dire, je ne suis pas très douée...).
Hey les amis ! Un petit coup de main ce serait vraiment super sympa...
(Autrement dit :"là, je galère à mort en ce moment" ^^).
Merci d'avance !
Tu crois que ça dialogue comme sur un "chat" ici ?
les réponses ne viennent pas en quelques secondes !!
c'est un forum.
 200 est une valeur exacte
200 est une valeur exacte
(on peut simplifier en 10 2)
2)
c'est justement ça qu'on appelle une "valeur exacte" : un truc écrit avec des symboles racines carrées et des nombres  écrits
écrits  et pas 3.14 et des fractions écrites en fraction 1/3 et pas 0.33 etc etc
et pas 3.14 et des fractions écrites en fraction 1/3 et pas 0.33 etc etc
mais en simplifiant les racines carrées tout de même !! (en "extrayant" les carrés qui sont dedans) et en simplifiant les fractions pour les écrire sous forme irréductible.
J'essayais juste en postant de remonter mon topic en haut de la liste, car je dois rendre cet exercice bientôt et suis bloquée sur une question.
Merci, mais je sais ce qu'est une valeur exacte. ce que je voulais dire c'est que √200 ou 10√2 ne sont pas des valeurs qui permettent de tracer le triangle.
mais c'est pas fini !!
tu gardes ces valeurs exactes jusqu'au bout
ce que tu cherches ce n'est pas OA c'est AE (en supposant que le sommet s'appelle E chez toi)
tu as donc déja un deuxième Pythagore à appliquer dans OAE pour obtenir AE (toujours en valeur exacte)
et ensuite tu traceras forcément une valeur approchée de AE
(mébof quelle importance de toute façon : ton 10cm de base il est déja imprécis au double décimètre. le reste serait donc du pinaillage)
maintenant je te rappelle aussi ce que j'avais écrit : ne faire aucun calcul du tout, parce qu'ils donneront forcément au final une valeur qu'on ne peut pas tracer "exactement" au double décimètre
si donc on veut une construction théoriquement exacte :
à partir de 10cm et de 6cm "réputés exacts" tu construis le triangle OAE "en vraie grandeur"
il n'y a pas besoin de connaitre la valeur, exacte ou pas, de AE pour ça !
et cette construction te donne la "valeur exacte" de AE, construite et tracée sur le dessin.
la suite est directe.
figure avec E appelé S :
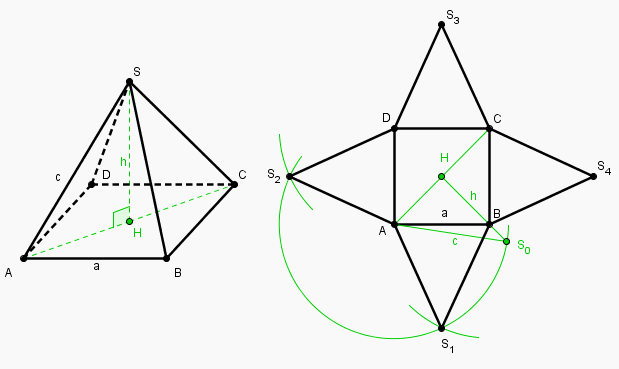
l'arète de la pyramide est construite à partir du carré ABCD (construit à la règle et au compas bien entendu) en portant HS0 = 6cm sur la demi-droite [HB)
le reste se termine au compas.


