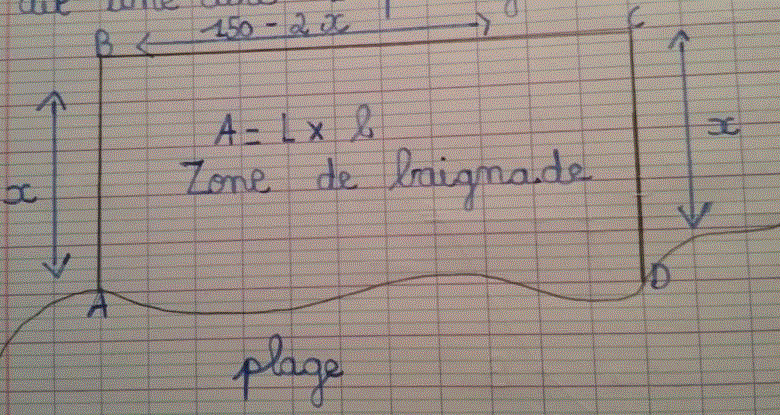Inscription / Connexion Nouveau Sujet
Le maitre nageur
Tony dispose de 150 m de lignes d'eau pour délimiter une zone de baignade rectangulaire. Il attend tes conseils pour que la zone de baignade ait une aire la plus grande possible.
Je n'arrive pas à résoudre cet exercice, merci de bien vouloir m'aider. (Je suis en 4ème.)
Ce n'est pas très grave si ce n'est pas systématique.
L'énoncé serait-il incomplet ? Car de ce qu'il y a marqué, plusieurs détails portent à confusion. Mais soit. Je répondrai à cet exercice comme je le comprends.
Je suppose que l'exercice met en scène une ligne d'eau qui délimite une zone de baignade isolée (sans contacts avec les bords extérieurs de la zone d'eau entière)

Il s'agirait ici de définir une largeur et une longueur des côtés d'un rectangle pour lequel son périmètre vaut 150 mètres, mais dont l'aire devra être le plus grand possible.
Trace plusieurs rectangles différents mais dont le périmètre vaut toujours 150 millimètres (ou 150 mètres si t'as la place ...), puis calcule leur aire. Détermine alors quel genre de rectangle serait le plus approprié.
en général, la zone de baignade est adossée à la plage, et donc le rectangle dessiné est la plage (sans ligne d'eau), 2 largeurs et une seule longueur
appelle x par exemple la largeur
tu en déduis la longueur puis l'aire
Bonjour, Merci pour vos explications, au début de l'énoncé on parle de tony qui est un maitre nageur sur la plage de Carnon. Je n'ai donc pas trouvé nécessaire de mettre ces informations. C'etait effectivement mon hypothèse d'utiliser les x, le rectangle n'est pas complet puisque en bas de la zone parallèle se situe la plage. La longueur parallèle du haut fait 150-2x (d'après ce que j'ai trouvé) et les 2 largeurs perpendiculaires sont des x.
ok, donc c'est bien ce que j'ai dit
tu connais donc tes deux dimensions du rectangle formé qui sont x et 150-2x
calcule l'aire de ce rectangle maintenant
Bonjour,
malou avait raison dommage pour le beau dessin de Arthur Thenon..
C'est un cas classique:
*Soit on calcule le maximum de x(150-2x ) en quatrième ?
*soit on teste comme tu dis entre 35 et 40 m...
*soit on sait que pour un périmètre égal ,le rectangle ayant l'aire la
plus grande est le carré et ici on aurait un demi carré.
Bonjour à tous,
malou avait raison dommage pour le beau dessin de Arthur Thenon..
d'où l'intérêt pour les demandeurs, et on ne le rabâchera jamais assez, de donner, dès le départ, l'énoncé complet avec les schémas éventuels au lieu de distiller petit à petit les informations nécessaires à la bonne compréhension de l'exercice.....
Bonsoir, excusez-moi, j'ai voulu me précipiter en donnant l'énoncé alors que j'avais oublié de donner ces informations elles aussi nécessaires. Merci à tous pour votre aide.
Pour calculer l'aire de mon rectangle je vais faire L×l= x × 150-2x
Pour les puristes:
Pourquoi parmi les rectangles ayant le même périmètre c'et le carré qui
aura l'aire la plus grande:
Soit un rectangle de largeur 1 m et de longueur 1.2 m.
aire = 1.2 m² son périmètre (1.2+1)*2= 4.4 m.
Nous pouvons construire un carré de coté 4.4/4 = 1.1 m
son aire sera 1.21 m² >1.2
Il faut généraliser:
Rectangle
largeur = a longueur = ka avec k>1
aire a²k périmètre 2 a(k+1)
le carré correspondant aura un coté = a(k+1)/2
et une aire de a²(k+1)²/4
comparons k avec (k+1)²/4 et nous voyons que k²+2k+1 > 4
puisque k>1 .
Savoir cela permet d'éviter la dérivée ou le calcul test dans
le problème du maître nageur:
Les 150 m de ligne d'eau formeront un rectangle par symétrie on aura un rectangle
de périmètre 150X2 =300 m dont on sait qu'un carré aura la meilleure aire donc....
Bonjour,
une malencontreuse erreur de frappe rend l'explication incompréhensible :
comparons k avec (k+1)²/4 et nous voyons que k²+2k+1 > 4
puisque k>1 .
k²+2k+1 > 4k est ce qu'il faut prouver !!
autre explication :
on veut comparer le carré de côté a de périmètre 4a et le rectangle de côtés a-x et a+x et donc de périmètre lui aussi 4a
et d'aire (a+x)(a-x) = a² - x²
à périmètre égal, l'aire du rectangle a² - x² sera toujours inférieure à celle du carré a²
(le carré x² étant toujours ≥ 0)
>mathafou
comme k est plus grand que 1 , c'est évident ,donc en se rapprochant de1
Posons k=1+ et donc comparé à(2+
et donc comparé à(2+ )²/4
)²/4
soit 4+4 +
+ ²/4
²/4
Et bien sûr cela confirme.
désolé mais prouver que k²+2k+1 > 4 ne prouve nullement qu'il est > 4k, vu que 4k est > 4
et c'est bien (k²+2k+1)/4 > k
soit k²+2k+1 > 4k
qu'il faut prouver.
que k soit posé 1 +  ou pas ne change rigoureusement rien à l'affaire.
ou pas ne change rigoureusement rien à l'affaire.
démonstration correcte :
on veut donc prouver que k² + 2k + 1 > 4k
soit à prouver que k² - 2k + 1 > 0
soit que (k-1)² > 0
et cette fois c'est bien vrai dès que k différent de 1 (> 1 ou même < 1 ça sera pareil)
Simplement pour ma satisfaction mentale:
le cas de k >1.1 par exemple est évident ,il faut prouver cette démo
pour k très proche de 1 d'où mon k=1+
on arrivait à k à comparer à (k+1)²/4
soit 4+4 à comparer à (2+
à comparer à (2+ )²
)²
on boit bien que le membre de droite est supérieur de  ².
².