Annuler
connectez vous
- Bissectrice et cercle inscrit dans un triangle - Cours 4ème
- Exercice Bissectrices et cercles inscrits dans un triangle
- Cours sur les Figures planes, Distance d'un point à une droite et Tangente à un cercle
- QCM : Figures planes, distance et tangente - Exercice 4ème
- Six Exercices de géométrie pure - quatrième
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques Collège cycles 3 /4On parle exclusivement de maths, niveau collège. QuatrièmeForum de quatrième GéométrieTopics traitant de géométrie [tout]Lister tous les topics de mathématiques
Niveau quatrième
le mileu dans un triangle
Posté par dark vergil (invité)
salut a tous et merci philoux de m'avoir repondu j'ai u bon a mon exercice mais maintenant j'ai un probléme de géometrie se serai cool si quelqun pouvai m'aider.
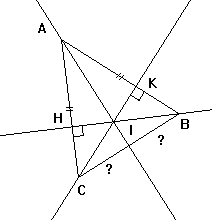
abc est un triangle isocéle de sommet principal a
les hauteurs(bh) et (ck) se coupent en i
pour la figure pas de probléme mais pour la question je fonce toujours dans le mur.la voici:
démontrer que (ai) coupe [bc]en sont milieu.
je suis aller voir la prof et elle veut pa m'aider.
merci encore de me donner un peu de votre temps.
Posté par gusgus6 (invité)re : le mileu dans un triangle
salut
tu peux faire un e figure s'il te plait
merci
gusgus la souris
Posté par gusgus6 (invité)re : le mileu dans un triangle
je t'explique normalement dans un triangle isocèle la hauteur qui passe par le sommet principal passe par le milieu du coté opposé a toi de voir
Posté par gusgus6 (invité)re : le mileu dans un triangle
je t'explique normalement dans un triangle isocèle la hauteur qui passe par le sommet principal passe par le milieu du coté opposé a toi de voir
Il y a plusieurs manières de justifier cela. As-tu appris dans ton cours que, dans un triangle isocèle, la hauteur issue du sommet principal était aussi médiane et médiatrice ?
I est l'orthocentre du triangle ABC (point de rencontre des hauteurs).
--> AI est une hauteur du triangle ABC.
--> angle AIC = angle(AIB) = 90° (1)
Soit K le point de rencontre de (AI) avec (BC).
Les triangles ACK et AIK sont rectangles en K
--> Pythagore:
AC² = AI² + KC²
AB² = AI² + KB²
Or AB = AC puisque le triangle ABC est isocèle en A --->
KC² = KB²
KC = KB
et donc K est le point milieu de [BC]
-----
Sauf distraction. 
Posté par dark vergil (invité)je n est pas apprit
bonjour à tous le monde et merci de m'aider.
mais il y a probléme j-p je n'est pas encore apprit le théoreme de pythagore.
execuse moi charmuzelle de pa avoir répondu avant.pour le dessin moi mes hauteurs elles sont un peu plus haute que toiet tu as coder que(ah)=(ak) mais on me le dis pas il faut que je le démontre sinon j'ai le mémme dessin que toi.
merci encore a vous tous de m'aider.
Euh non, le codage initial indique que AB=AC, c'est tout, mais il y a superposition avec le dessin des hauteurs.
I étant le point d'intersection des hauteurs (BH) et (CK), on déduit que (AI) est la troisième hauteur du triangle, puisque les trois hauteurs d'un triangle sont concourantes en son orthocentre .
Donc (AI)et (BC) sont perpendiculaires. (AI) est la perpendiculaire à (BC) qui passe par A.
AB=AC (triangle isocèle en A), donc A est sur la médiatrice de [BC]
(si un point est équidistant des deux extrémités d'un segment, alors il est sur sa médiatrice)
La médiatrice de (BC) passe donc par A, et, comme toute médiatrice, est perpendiculaire au segment. La médiatrice de [BC] est donc la droite qui lui est perpendiculaire te qui passe par A. Tiens ? C'est donc (AI)
Comme la médiatrice d'un segment est la droite qui lui est perpendicualire et passe par son milieu , tu en déduis que (AI) coupe [BC] en son milieu. CQFD (ce qu'il fallait démontrer)