Inscription / Connexion Nouveau Sujet
Lecture graphique
Bonjour est ce que vouS pouvez m'aider à résoudre cet exercice s'il vous plait ?
Voici l'énoncé :
On considère une fonction f définie et dérivable sur l'intervable [-2;4].
On note f' la fonction dérivée de la fonction f .
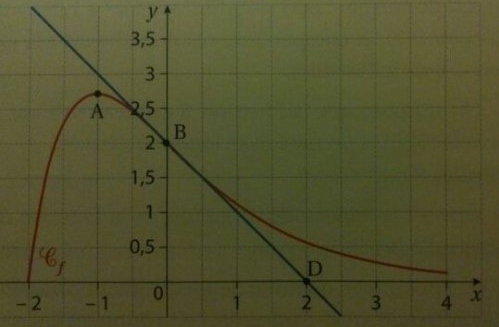
La courbe Cf' tracée ci-dessous, représente la fonction f dans le plan muni d'un repère orthogonal.
La courbe Cf passe par les points B (0;2) et A d'abscisse -1 .
Elle admet au point A une tangente parallèle à l'axe des abscisses.
La tangente T à la courbe Cf au point B passe par le point D(2;0) et traverse la courbe en B.
1/En utilisant les données graphiques, indiquer:
a)le nombre de solutions sur l'intervalle [-2;4] de l'équation f(x)=1 et un encadrement d'amplitude 0.5 des solutions éventuelles;
b)la valeur de f'(-1);
c)l'équation de T
d)la valeur de f'(0)
e)le signe de la dérivée f' de la fonction f sur l'intervalle [-2;4];
f)si la courbe Cf admet un point d'inflexion;
g)la convexité de la fonction f.
Merci d'avance de votre aide j'en ai vraiment besoin
Bonjour,
revoir l'énoncé, les données que tu as mises ici sont incohérentes.
"et A d'abscisse -1" par exemple.
Vérifier toutes tes coordonnées etc .
et j'ai eu beau chercher sous mon écran, je n'ai pas trouvé "La courbe tracée ci-dessous"
J'ai vérifié les données que j'ai mis et elles sont exactes...
Et j'ai essayé de mettre une photo de la courbe mais ça me la pas afficher 
Est ce que vous sauriez comment faire ? svp
Non. sans donnée fiable aucune chance de faire :
En utilisant les données graphiques
"le point A d'abscisse -1" est complètement aberrant
d'abord parce qu'un point a DEUX coordonnées, donc à moins de préciser autre chose sur ce point A, on peut le placer n'importe où sur la droite verticale x = -1, ce qui donne une infinité de courbes répondant à ces données là, et rendant impossible de répondre à quelque question que ce soit.
Pour mettre une figure c'est facile : le bouton Img puis un peu plus bas les champs "parcourir" et le bouton ATTACHER.
l'image doit être une image.
pas une photo au format affiche de cinéma en dizaines de millions de pixels.
On fait des images parfaitement claires et nettes avec 400x400 pixels.
après, le mode d'emploi de ton scanner/appareil photo/logiciel de retouche d'image, aucune idée, c'est toi qui sait.
Ah bein voila elle est arrivée pendant que je tapais ma réponse !
question a)
il s'agit de lire sur le graphique le nombre de points d'intersection de la courbe avec la droite y = 1
b) la valeur de f'(-1) est indiquée dans l'énoncé, il suffit de savoir le lire et de savoir ce que représente f'
c) équation d'une droite passant par deux points connus
d) f'(0) est déduit de ce que tu obtiens à la question c.
e) le signe de la dérivée est déduit du sens de variation de f(), lu sur le graphique
f) définition d'un point d'inflexion. (voir cours)
g) définition de la convexité (voir cours)
merci de ces réponses mais justement je ne sais plus lire f' sur une courbe
vous pourriez me rappeler comment on fait svp ?
???
quel est le point d'abscise -1 sur la courbe ? (c'est dit dans l'énoncé)
quelle est la tangente en ce point ? (c'est aussi dit dans l'énoncé)
la pente de cette tangente là en ce point là ????
pour abscisse -1 c'est (0;2)
La tangente en ce point passe par le point D (2;0)
mais après je sais plus comment on fait pour calculer cette tangente
je crois qu'il faut faire : (mouvement horizontale / mouvement verticale) pour obtenir la dérivée
mais je suis pas sur du tout c'est ça mon souci 
La courbe Cf passe par les points... et A d'abscisse -1 .
Elle admet au point A une tangente parallèle à l'axe des abscisses.
il n'y a rien à calculer, juste savoir lire un énoncé.
tu auras bien assez des questions suivantes pour calculer...
pour abscisse -1 c'est (0;2)
abscisse - 1 c'est (
c'est quoi quoi ce (0;2) ???
le point (
sans doute, à peu près, on n'en sait rien. tu cherches midi à quatorze heures.
Mais par contre c'est le point A et il est dit dans l'énoncé quelle était la tangente en ce point, en particulier sa pente : elle est parallèle à l'axe des abscisse !!!
donc f'(-1) est donné dans l'énoncé !!! c'est 0 la pente d'une droite parallèle à l'axe des abscisse. f'(-1) = 0.
Pour la réponse c comment faut il faire pour trouver l'équation. Alors ?
Y a t'il des calculs , formules à appliquer ?
oui il y a des formules, mais avant d'appliquer quelque "formule" que ce soit il faut bien comprendre ce que l'on cherche !!
Là aussi il faut lire et comprendre l'énoncé :
La tangente T à la courbe Cf au point B passe par le point D(2;0)
la tangente cherchée est la droite BD, un point c'est tout.
B(0;2) est donné dans l'énoncé
D(2;0) aussi
oublies donc toute histoire de Cf et de tangente et cherches l'équation de la simple droite qui passe par ces deux points.
C'est tout.
et ce sera la tangente !
Pour trouver l'équation d'une droite qui passe par deux points donnés il y a diverses méthodes, au choix.
je t'en donne une qui marche ici (et même souvent) très bien :
l'équation générale d'une droite est y = ax + b
la droite cherchée passe par B(0;2) donc 2 = a.0 + b => b = ?
la droite cherchée passe par D(2;0) donc 0 = a.2 + b
b on vient de le calculer, donc on trouve a = ?
et c'est fini.
2 = a.0 + b ça donne b = 2 !!! pas 0 !!
ensuite 0 = a.2 + 2 donne bien a = -1, OK mais tu as dû obtenir ça autrement ?!
et l'équation de la droite y = ax + b est donc y = -x +
pour la question d'après tu n'as rien à remplacer du tout.
f'(0) c'est la pente de la tangente à la courbe en le point B
quelle est cette tangente ? tu viens d'en calculer l'équation de cette tangente !
quelle est donc la pente de la droite dont tu viens de calculer l'équation y = -x + 2 ??
la pente de y = ax + b c'est le coeficient de x : a !!
ici y = -x + 2 le coeficient de x c'est combien ???
la droite étant la tangente en B(0; 2) sa pente est la dérivée f' en ce point c'est à dire f'(0)
donc f'(0) c'est -1. finie la question
tu attends que je te relise l'énoncé et les messages précédents à chaque valeur individuelle que tu vas calculer pour savoir pourquoi on l'a calculée ??
question suivante.
signe de f'(x) sur l'intervalle [-2; 4]
e) le signe de la dérivée est déduit du sens de variation de f(), lu sur le graphique
donc tu regardes sur le graphique comment varie la fonction sur cet intervalle, c'est à dire tu lis sur le graphique pour chacun des "morceaux" si elle est croissante ou décroissante et tu reconstitues ainsi un tableau de variation.
Qui te donne le signe de la dérivée dans chacun des morceaux de cet intervalle :
si la fonction est croissante dans ce morceau d'intervalle f'x) est >0 dans ce morceau, si elle est décroissante, f'(x) est < 0
si elle passe par un extrèmum (ici un maximum) f'(x) = 0 pour cette valeur de x
allez je te donne 5 minutes p.
il n'y a qu'à regarder le graphique
1) sauf qu'on te demande dans [-2; 4] parce que en dehors de cet intervalle il n'y a pas de graphique, donc tu ne peux avoir aucune idée sur f(x) et f'(x) en dehors de [-2; 4]
rien ne te dis que la fonction ne va pas remonter apres x = 25 etc
2) d'autre part tu as des valeurs FAUSSES
en x = -1 f(x) ne vaut pas 0 et
en x = -1 f'(x) est parfaitement définie, et c'est elle qui vaut 0
X: - -1 +
f(x) : croissante Décroissante
f´(x): + -
la valeur exacte de M = f(-1) n'est pas connue
la seule chose qu'on peut dire c'est qu'elle est aux environs de 2.7, lue sur le graphique.
(et puis la fonction s'appelle f, pas F. petit détail, mais autant utiliser les notations de l'exercice et pas d'autres à toi)
Oui autant s'exprimer correctement c'est vrai
Merci de votre aide en tout cas
Est ce que pour la question suivante le point d'inflexion est B c,est à dire (0;2) ?
exactement. c'est la définition :
en ce point la courbe traverse sa tangente, c'est marqué dans l'énoncé en plus.
D'accord merci beaucoup
Par contre j'ai oublier d'écrire une toute petite question qui est :
2) parmi les trois courbes suivantes qu'elle est celle qui peut représenter la courbe de la dérivée f´ de f ?
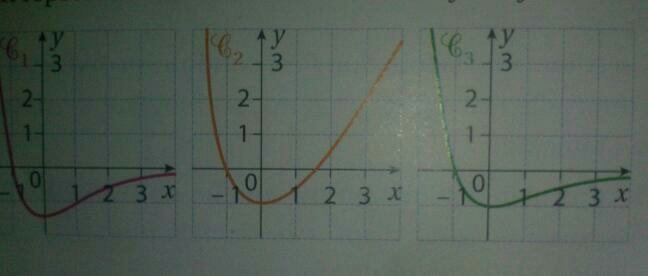
que sais tu de la dérivée ?
f'(-1) = 0 : les trois courbes sont OK sur ce point là
f'(0) = -1 : quelles sont les courbes candidates qui restent ?
f'(x) s'anulle-telle ailleurs qu'en -1 dans l'intervalle [-2;4]
que reste-t-il comme courbe possible ?
sinon tu as aussi oublié de parler de la concavité :
la concavité change aux points d'inflexion
elle est vers le bas dans [-2;0]
vers le haut dans [0;4]
C'est la verte alors oui 
Oui la concavité j'avais réussi à le faire seule alors j'ai préférer ne pas vous embêter avec cette question 


 -1 +
-1 +


