*au niveau de la mer

Fais déjà une figure en coupe
avec un observateur S placé à une hauteur x
au-dessus de la terre que l'on suppose ronde ;
l'observateur S regarde vers l'horizon ;
son regard vient tangenter le cercle Terre en T et T'

Merci de ton aide!

Voici la figure en coupe. Mais malheureusement cela ne me permet toujours pas de pouvoir poser l'équation, trop de points encore inconnus. Est-ce que ce triangle pourrait être un équilatéral au quel cas nous pourrions utiliser la formule qui dit que la hauteur de ce dernier est égal à ?

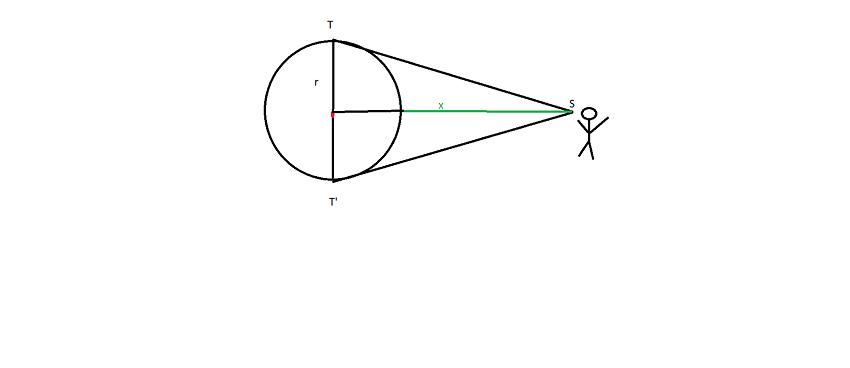
Y'a du mieux.

Rapproche maintenant le point S du cercle terre.
Tu verras que T et T' sont symétriques ; pour autant
ils ne sont pas diamétralement opposés comme semble
le laisser supposer ta figure.

SI on appelle O le centre de la terre de rayon R
les triangles STO et ST'O sont des triangles rectangles.

Bonsoir,
un dessin plus raisonnable :

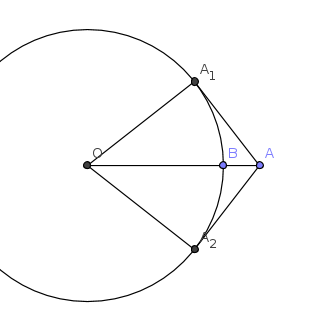
Les triangles (OA₁A) et (OA₂A) sont rectangles.
AB=x et OA₁=OA₂=OB=r

AH! Oui merci !
Je vois où je dois me diriger. Il faut très certainement utiliser la formule de la calotte. A=2rh

toutafé

Mais donc ! Est-ce que c'est juste de dire que la hauteur h de la calotte est égale à (r-x)/2 ?
Et donc que ?

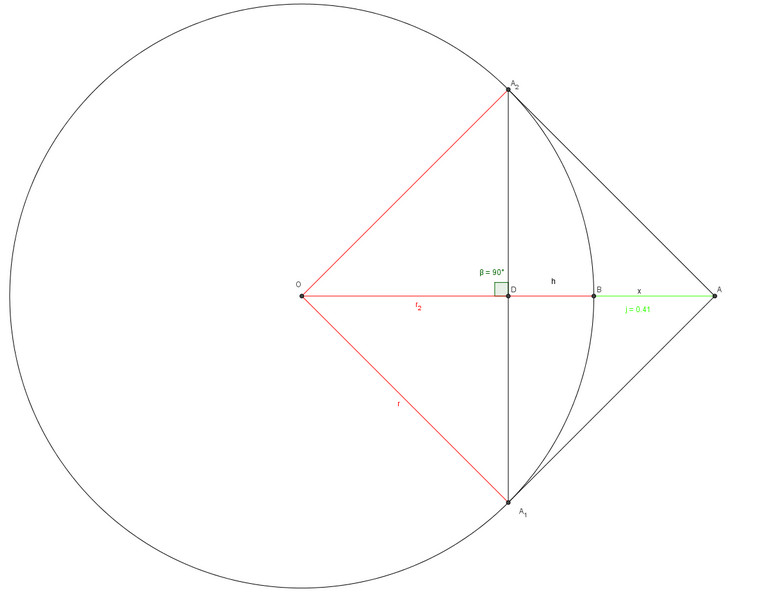
Bonjour

faire la figure dans un cas aussi particulier que celui là ne permettra pas de faire des calculs sérieux ...
( = sans être influencé par des valeurs numériques complètement fausses dans le cas général)

ton énoncé dit 1/n de la surface
pas une valeur numérique !
donc le résultat sera fonction de n.
l'angle des tangentes (ou des rayons qui leur sont perpendiculaires) est variable et fonction de n

par ailleurs ta figure est illisible parce que l'export direct d'une figure par Géogebra fait ça (textes microscopiques et illisibles ou au contraire monstrueusement énormes, point moches de taille indéterminée etc etc

personnellement je n'utilise jamais l'export de figure
je fais une copie de zone d'écran (indépendamment de Géogebra)
c'est infiniment plus instantané et plus fiable que de régler et bidouiller les paramètres interdépendants d'exports en image de Géogebra !

Oui, je suis d'accord.
Par contre ça m'aide juste à me représenter grossièrement de quoi on parle..

Et du coup je voulais juste savoir comment calculer la hauteur de la calotte comme précédemment indiqué dans mon dernier post.

Merci de vos réponses !

Soit H le projeté orthogonal du point A1 sur la droite (OA).
La hauteur de la calotte sphérique BH est égale à  AH - AB .
AH peut être calculé en fonction de  x  et de  R  dans le triangle AHA1.