Bonjour,
Où en es-tu?
Quels points as-tu choisis?

voici où j'en suis :
1. Graphique : a, b
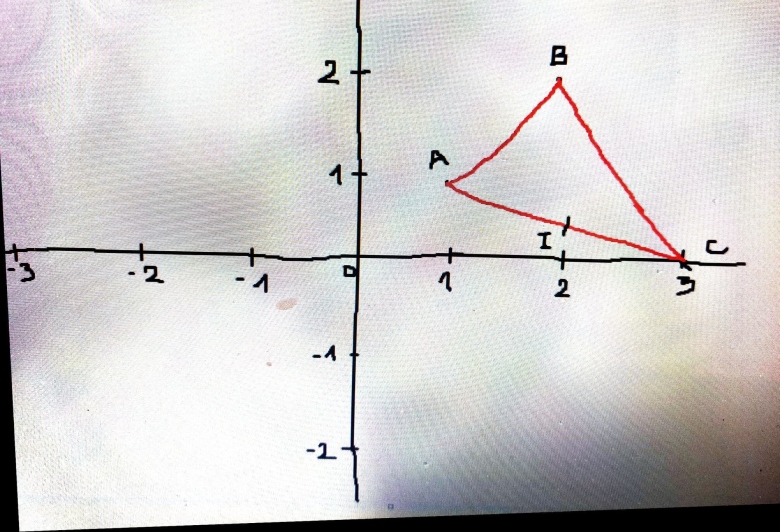
c. Les coordonnées exactes des points sont :
- A : (1;1)
- B : (2;2)
- C : (3;0)

Que proposes-tu pour calculer les coordonnées de I?

c) Calculer les coordonnées du point I milieu de [AC].

A(1;1) et C(3;0)
On a xI = 1 + 3 /2 = 2 et yI = 1 + 0 /2 = 0,5
Par conséquent I (2; 0,5).

Oui.
Maintenant que tu as ces cordonnées du milieu d'une diagonale, quelle propriété des parallélogrammes penses-tu utiliser pour déterminer les coordonnées du point D?

Les diagonales [AC] et [BD] d'un parallélogramme ABCD se coupent en leur milieu.

Oui. I est donc aussi le milieu de ...???

I est donc aussi le milieu de [AC]

Non. Ça,  c'est la définition de I:

ok,
I est donc aussi le milieu de [BD]

Oui.
Et donc, il existe deux vecteurs égaux.
Cette égalité devrait te permettre de trouver les coordonnées de D

D'accord,
b) Soit I le milieu commun des diagonales [AC] et [BD] du parallélogramme ABCD.

I étant aussi le milieu de la diagonale [BD], on a :
xI = xB + xD /2      et    yI = yB + yD /2
2 = 2 + xD /2            0,5 = 2 + yD /2
4 = 2 + xD                 1 = 2 + xD
4 - 2 = xD                 1 - 2 = yD
     2 = xD                     -1 = yD

Les coordonnées de D tel que ABCD soit un parallélogramme sont (2 ; −1).

En attendant la correction du b, j'ai continué la suite.

c) Voir le graphique (j'ai placé le point D sur le 2 abcisse et -1 ordonnée)

3. Calculer des longueurs :

a) Calculer les longueurs des 4 côtés (AB, BC, CD et DA) :

A(1;1) B(2;2) C(3;0) D(2; -1)

AB² = (2-1)² + (2-1)²
AB² = 1² + 1² = 1 + 1 = 2
AB = √2

BC² = (3-2)² + (0-2)²
BC² = 1² + (-2)² = 1 + 4 = 5
BC = √5

CD² = (2-3)² + (-1-0)²
CD² = (-1)² + (-1)² = 1 + 1 = 2
CD = √2

DA² = (1-2)² + (1-(-1))²
DA² = (-1)² + 2² = 1 + 4 = 5
DA = √5

b) Calculer les longueurs des diagonales (AC et BD) :

La diagonale AC :
AC² = AB² + BC²
AC² = 2² + 0,5²
AC² = 4 + 0,25
AC² = 4,25
AC² = √4,25
AC = 2,06
La longueur de la diagonale AC est de 2,06 cm.

La diagonale BD :
BD² = AD² + DC²
BD² = 2² + (-1)²
BD² = 4 + 1
BD² = 5
BD² = √5
BD = 2,24
La longueur de la diagonale BD est de 2,24 cm.

OK pour les longueurs des côtés.
Pas pour les diagonales. Ne confonds pas 0.5 et 5. D'où sort le (-1)² ?
Et même si le résultat était 4.25 ou 5, il n'y a aucune raison d'en calculer une valeur approchée.

La diagonale AC :
AC² = AB² + BC²
AC² = √2² + √5²
AC² = 2 + 5
AC² = 7
AC² = √7
AC = 2,65
La longueur de la diagonale AC est de 2,65 cm.

La diagonale BD :
BD² = AD² + DC²
BD² = √5² + √2²
BD² = 5 + 2
BD² = 7
BD² = √7
BD = 2,65
La longueur de la diagonale BD est de 2,65 cm.

Donc, si j'ai bien compris le résultat 2,65 je supprime c'est inutile ?

Oui, c'est inutile.
Tes calculs sont faux car tu n'es pas dans des triangles rectangles.
Calcule AC et BD comme tu l'as fait pour les côtés du parallélogramme. Avec les coordonnées des extrémités...

D'accord,

A(1;1) B(2;2) C(3;0) D(2; -1)

La diagonale AC :
AC² = (3-1)² + (0-1)²
AC² = 2² + (-1)²
AC² =  4 + 1
AC² = 5
AC = √5

La longueur de la diagonale AC est de  √5 cm.

La diagonale BD :
BD² = (2-2)² + ((-1)-2)²
BD² =  0² + (-3)²
BD² = 0 + 9
BD² = 9
BD² = √9
BD = 3

La longueur de la diagonale BD est de 3 cm.

Oui

Merci

4. Conjecture :

a) Calculer la somme des carrés des côtés :
Somme des carrés des côtés = AB² + BC² + CD² + DA²
                                                    = √2² + √5² + √2² + √5²
                                                    = √14²
                                                    = √196
                                                    = 14

b) Calculer la somme des carrés des diagonales :
Somme des carrés des diagonales = AC² + BD²
                                                               = √5² + 3²
                                                               = √25 + 9
                                                               = 5 + 9
                                                               = 14

b) Je remarque que l'on arrive au même résultat.
(après Proposer une utilisation de Geogebra ? comment mit prendre avec ça pour l'argumentation ?)

Je n'ai jamais pratiqué ce genre de question dans ma scolarité. Le ordinateurs n'existaient pas. Géogébra non plus.
On ne te demande pas une preuve mais un "appui" de ta conjecture.
Tu peux faire ton dessin sur Géogebra.
Évite de mettre un point sur un axe car après il y est lié. Tu ne peux le déplacer que sur l'axe.
Tu crées 3 points
Tu places I le milieu de AC
Tu traces le vecteur
Tu place un représentant de ce vecteur qui démarre en I
Ça te donne D
Tu calcules le carré des distances et les sommes de l'énoncé.
Tu fais bouger A et/ou B et/ou C et tu constates l'égalité

Merci pour votre réponse sincère mais de mon côté je n'arrive jamais avec Géogébra, serait-il possible d'avoir l'image et puis je la dessinerais moi-même sur une feuille s'il vous plait.

Voici l'argumentation :
b) Je remarque que l'on arrive au même résultat.
On peut dire de l'égalité que la somme des carrés des quatre cotés est égale à la somme des carrés des diagonales, augmentée de quatre fois le carré de la distance entre les milieux des diagonales.

?

Enfaite je voulais parler des diagonales quand elles sont coupée en leur milieu...donc j'ai compris que ça doit être supprimer.

b) Je remarque que l'on arrive au même résultat.
On peut dire de l'égalité que la somme des carrés des quatre cotés est égale à la somme des carrés des diagonales.

Oui.
Pour Géogébra, je vais demander si quelqu'un en sait plus sur ce qui est attendu...

Bonjour
personnellement, je ferais afficher à geogebra d'une part la somme AB² + BC² + CD² + DA² et d'autre part la somme AC² + BD² l'une sous l'autre

Merci sanantonio312 pour tout ton aide.

Bonjour malou et merci pour ta présence
comme j'ai dit dans un de mes messages pour géogébra si c'est possible d'avoir l'image et puis je la dessinerais moi-même sur une feuille s'il te plait car j'ai trop de mal à l'utiliser.

ah ben non...ça marche pas comme ça
si tu refuses sans cesse de l'utiliser, tu ne sauras jamais le faire
en plus je serais ton prof, je demanderais que tu m'envoies le fichier geogebra pour vérifier que tu as tout bien fait

commence par tracer un parallélogramme ABCD dans geogebra
dis moi comment tu t'y prends

Bonjour,

ça ne rime à rien une image sur papier/photo/copie d'écran de la figure Geogebra !
parce que la seule différence entre ta figure (déja faite) et Geogebra est qu'on peut déplacer les points A, B, C à volonté
et que Geogebra déplace I et D (si on les a construits et pas simplement placés) et refait les calculs.

si tu refuses d'utiliser, et même d'essayer d'utiliser, Geogebra tu n'as qu'une seule façon de faire sans :

refaire d'autres figures (plusieurs) sur papier en choisissant d'autres positions pour A, B, C au hasard et refaire les calculs avec chacune de ces autres positions ...
bon courage ...

ça ira plus vite de réussir à utiliser Geogebra : c'est plus facile que de nombreux jeux vidéo ...

Cela ne veut pas dire que je n'ai jamais essayé sinon je ne dirais rien. Justement je l'avoue je n'y arrive pas tout simplement et avoir des réponses à l'écris c'est encore loin de comprendre ( la facilité est du directe là  peut-être ça sera plus facile). Je ne doute pas que avec Geogebra ça ira plus vite  mais bon je vais encore tenter. Je vais déjà commencer par tracer un parallélogramme ABCD comme me l'a proposé malou.
Justement même les jeux vidéos je ne suis pas dessus , ça ne m'intéresse pas puis on est pas tous pareil...

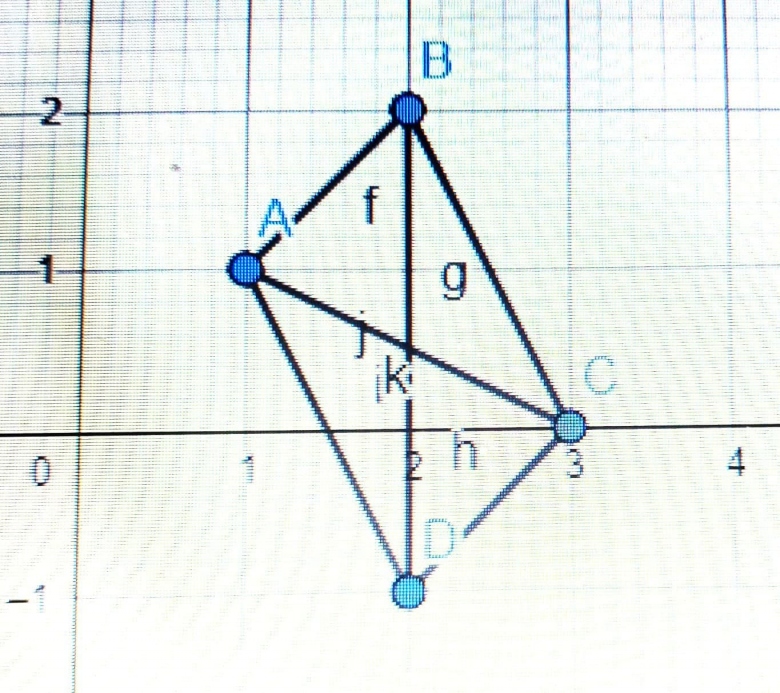
Voici le parallélogramme ABCD (juste une petite chose je n'ai pas pu enlever les lettres qui se sont mit sur la figure "h, i, j ,k ,f et g")

bien
visiblement tu n'as pas construit ça comme tu l'avais construit à la main sur papier :
choisir trois Points A,B,C (pas 4)
construire le milieu I de BC etc
la construction est exactement la même que la construction à la main.

ce qui est absolument fondamental est que seuls trois points A, B, C sont "libres"
tout le reste doit suivre
et pas placer les 4  sommets de ce qu'on croit être un parallélogramme
(les 4 points libres)

parce que l'intérêt de Geogebra n'est certainement pas de refaire la même figure avec les points au même endroit que la figure sur papier !
(aucun intérêt à part vérifier ses calculs numériques)

mais de déplacer à volonté les points A, B, C pour vérifier la conjecture dans plusieurs cas
si D ne suit pas automatiquement (car D a été construit et pas placé) pour que ça donne toujours un parallélogramme, c'est raté.

pour enlever les noms des segments, accéder à leurs propriétés et "cacher l'étiquette".
tant qu'à faire les renommer en AB, BC etc

une copie d'écran de ce que l'on peut avoir
en affichant en plus le protocole de construction


(l'aspect et la disposition varie selon les versions de Geogebra)

D'accord, merci beaucoup mathafou, je vois mieux et je comprend ce que tu veux dire au niveau du  protocole de construction.

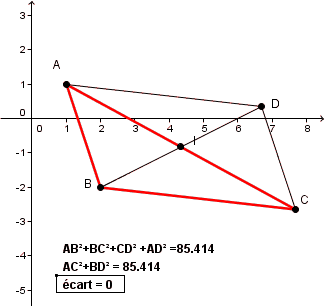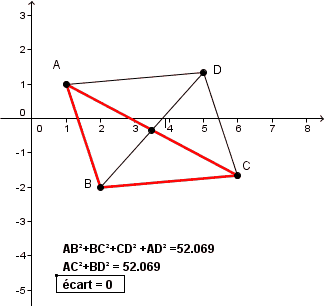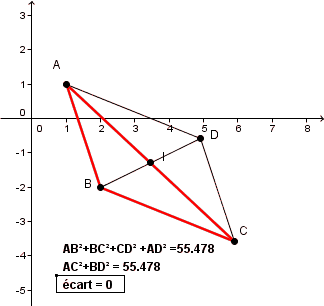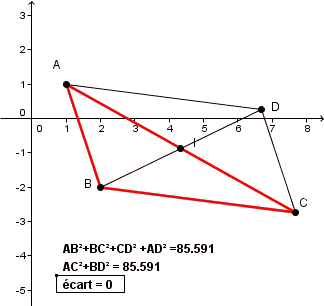
et le résultat c'est d'observer (conjecture) les valeurs affichées de AB²+BC²+CD²+AD² par rapport à celles de AC²+BD² quand on déplace les points A, B, C
(ou la différence (AB²+BC²+CD²+AD²) - (AC²+BD²))

une petite animation (sur le fichier Geogebra précédent) :



déplacer les points à la main suffira dans l'exo !

Merci beaucoup mathafou
Si j'en fait 3 de dessin à chaque déplacement  des points ça ira ?

ça me semble raisonnable de "conserver" 3 positions

mais en fait tu en fais réellement des dizaines en un rien de temps vu que le simple déplacement d'un point quelconque A, B ou C à la souris se fait en une fraction de seconde et c'est Geogebra qui fait tout le boulot pour suivre ce déplacement et recalculer tout.

au besoin tu pourras même en "fournir" une quasi infinité : le fichier Geogebra lui-même !

d'accord, merci