Inscription / Connexion Nouveau Sujet
lieu géometrique
bonjour a tous , est ce que quelqu'un pourrait m'aider sur ce probleme
on considere un cercle C de centre O et de rayon 8
A est un point fixé à l'interieur du cerlce
une equerre aAPQ dont l'angle droit est fixé en A tourne autour de ce point
on a aussi AP=16 et AQ=27
le coté [AP] coupe le cercle (C) en E et le coté [AQ] coupe ce meme cercle en R
M milieu de [EF]
voila la figure obtenue
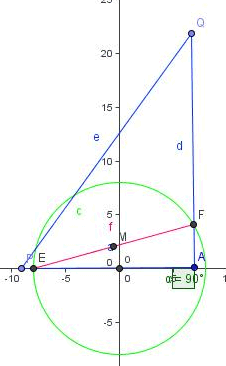
1)on cherche a caracteriser le lieu (G) de M
2)on admet provisoirement que M est caracterisé par OM²+AM²=64
déterminer alors l'ensemble(G)
3)démontrer l'égalité de la question 2 ( a l'aide du theoreme des médianes)
édit Océane : image placée sur le serveur de l'
Bonjour,
1) un petit dessin:
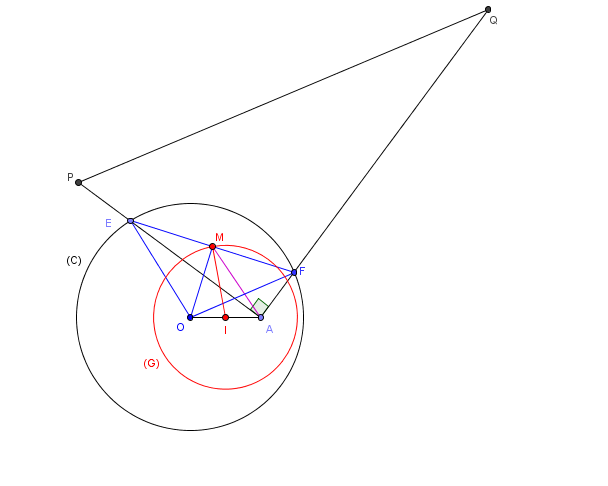
2) Soit I le milieu de
Le théorème de la médaine dans le triangle donne:
avec
car
est intérieur à
soit .
Le lieu est donc le cercle de centre
et de rayon
C' est un début...
3) On applique le théorème de la médiane dans les 2 triangles et
:
Oe le triangle est rectangle en
et
d' où: .
merci pour ton aide mais je comprends pas trop comment tu passe de
la 2 a la 3 ligne pour la question 3 ( comment tu fait disparaitre le 2 au dénominateur de EF²)
Les 2 lignes sont indépendantes:
La première donne la quantité en fonction de
,
et
La seconde montre avec Pythagore que
Si cette quantité est nulle, sa moitié l' est aussi et
? mon post est dans fonctions ; minorant , majorant .
Annuler
connectez vous