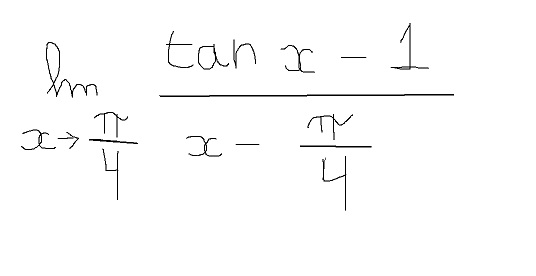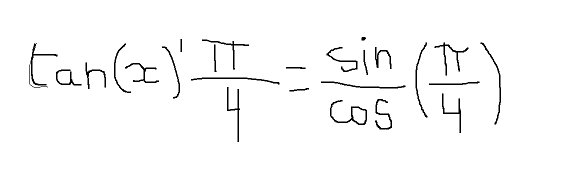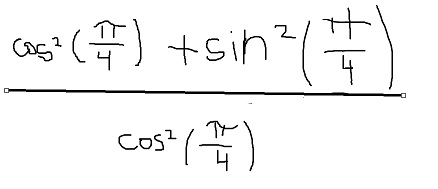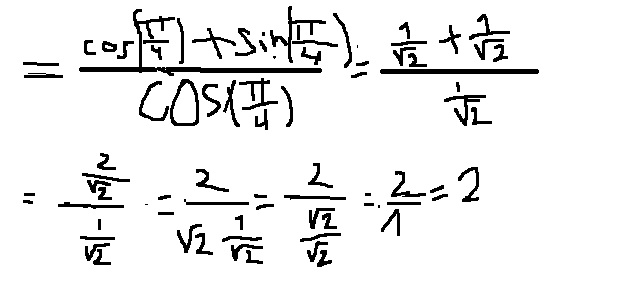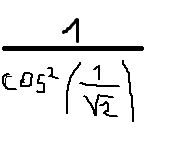Inscription / Connexion Nouveau Sujet
limite avec tan et pi
bonjour,
pouvez vous m'aider avec cette limite?
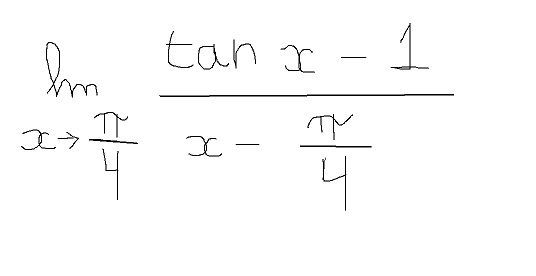
ça ressemble énormement à la définition de la dérivé de tan x en pi/4
mais je suis vraiment coincé
merci de votre aide,
ça ressemble énormement à la définition de la dérivé de tan x en pi/4
mais je suis vraiment coincé
merci de votre aide,
Bonsoir,
En effet, ça ressemble énormément à la définition du nombre dérivé de tan en pi/4 (d'ailleurs tan y est bien dérivable, ouf) ...
Maintenant que tu as vu ça... c'est quasiment terminé !
Que vaut tan'(pi/4) ?
merci ,tan pi/4 vaut 1 donc on change le 1 du numerateur par tan pi/4 et on a la definition de la derive de tan en pi /4
et maintenant comment je fais la dérivé de tan'(pi/4) ?
pouvez-vous m'aider à faire tan'(pi/4)
Si tu ne connais pas une expression de tan', tu peux écrire tan(x)=sin(x)/cos(x) puis te ramener à dériver un quotient...
Attention, il faut éviter d'écrire « tan(x)' ». « tan'(x) », c'est mieux (vu que ce qu'on dérivé, c'est la fonction tan, pas le nombre « tan(x) »...).
Bref, commence par trouver une expression générale de tan'(x), que tu pourras ensuite évaluer en pi/4 (ça y est dérivable donc pas de soucis).
tan = sin/cos
or (u/v)' = (u'v-v'u)/v², donc tan'(x) = ......
on obtient
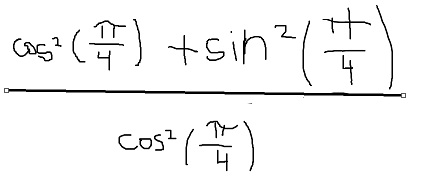
que cela est bien égal à sin^2(pi/4)
et on laisse comme ça ou on peut simplifier?
je remercie votre aide
Oui, c'est bien ça (si on doit bien lire un cos² au dénominateur).
... mais ça peut encore se simplifier !
— déjà, au numérateur, tu as quelque chose de la forme cos²(x)+sin²(x)... et ça ça vaut 1 !
— pi/4, c'est un angle « gentil » : tu dois connaître les valeurs de son sinus et de son cosinus...
Après simplification, normalement tu devrais trouver 2.
Attention, au début tu as des cos² et des sin²... et après ils se transforment en cos et sin comme par magie !
Deuxième point également, ne t'embête pas avec le numérateur : cos²(x)+sin²(x), ça fait 1 quelque soit le réel x que tu considères, c'est une identité trigo à connaître par cœur !
Pour s'en convaincre :
cos²(x) + sin²(x)
= cos(x)cos(x) + sin(x)sin(x)
= cos(x)cos(-x) - sin(x)sin(-x) car cos paire et sin impaire
= cos(x-x)
= cos(0)
= 1.
Attention...
Ce que tu obtiens n'est pas 1/cos²(1/V2) mais 1/cos²(pi/4).
Et 1/cos²(pi/4), c'est 1/[cos(pi/4)]².
Où tu connais la valeur de cos(pi/4), c'est 1/V2.
Moralité : on obtient 1/[1/V2]² = 1/[1/2] = 2.
Bref, reprends ce calcul à tête reposée... je suis persuadé que tu es tout à fait capable de faire ce calcul, mais à ces heures tardives, c'est moins facile.