Inscription / Connexion Nouveau Sujet
Limite de fonction
Bonjour,
j'ai un exercice pour mon dm de maths mais je n'ai pas tous compris.
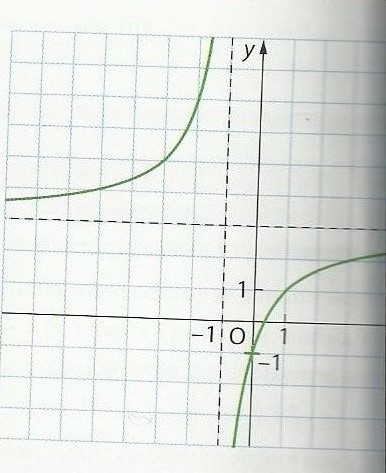
Le graphique ci-dessous donne une partie de la courbe représentative d"une fonction homographique f et des ses deux asymptotes.
On suppose que f(x) est de la forme (ax+b)/(x+c). La fonction f est définie pour tout nombre x sauf pour une valeur associé à l'asymptote verticale.
a) Determiner graphiquement cette valeur
b) déduisez-en la valeur de c.
C'est déjà une premiere partie des questions que je n'ai pas compris.
Merci de votre aide
La valeur de x associée à l'asymptote verticale, c'est - 1 , comme on le voit sur le graphique.
La présence d'une asymptote verticale montre que - 1 est une valeur interdite pour x . Si x prenait cette valeur, le dénominateur s'annulerait, et on n'a pas le droit de diviser par 0.
Tu dois pouvoir déduire de ce qui précède la valeur de c .
Merci beaucoup pour votre aide.
Par contre, la prochaine question je n'ai pas compris puisque c'est:
2) La courbe admet une asymptote horizontale qui nous permet de déterminer, par exemple la limite de f en +
a) Determinez graphiquement limf(x) lorsque x tend vers +
Pour cette question j'ai répondu que la limite de f(x) est +
b) Deduisez-en que a est non nul et déterminez sa valeur
Je n'ai pas réussi à répondre à celle-ci..
2)a) Non, la limite de f(x) n'est pas + oo. Elle est égale à l'ordonnée de l'asymptote horizontale (regarde le graphique).
très bien merci beaucoup de votre aide.
J'ai juste une dernière question et après je vous laisse tranquille.
Il reste à determiner la valeur de b. Il suffit pour cela de connaître les coordonnées d'un point de la courbe.Or l'ordonnée du point d'intersection et de l'axe des ordonnées est égale à -1. Determinez b
Moi j'ai placé un point A( -1,0) et B(1;1) j'ai fait (Yb-Ya)/(Xb-Xa) et j'ai trouvé 1/2 est ce correct ?
Je ne comprends pas ce que tu as fait.
Si une une courbe d'équation y = f(x) passe par un point M(xM; yM), c'est que les coordonnées de ce point vérifient l'équation de la courbe.
On peux donc écrire yM = f(xM).
Dans le cas présent, cette égalité permet de calculer b .
Choisis comme point le point B(1; 1). Quant au point A(- 1; 0) ??? - 1 est la valeur interdite pour x !
Effectivement je n'avais pas pensé à cela..
Je dois donc créer le point A(1;1) et cela verifie l'équation yB=f(xB) et cela me donnera la valeur de b ?
En faisant à tête reposé j'ai choisi un point A(-4;4)
donc Ya=f(Xa)
-4=(3*4+b)/3
b=-1
est-ce correct cette fois-ci ?
Résultat exact, quoique le point (- 4; 4) ne paraisse pas appartenir la courbe. D'ailleurs, c'est le point (4; - 4) que tu as pris dans ton calcul . . . .
Pourquoi ne prends-tu pas le point (1; 1) ?