Inscription / Connexion Nouveau Sujet
Limite et dérivée: Tableaux de variation
Bonjour,
Dans le cas de mon DM je dois étudier les variations de la fonction:
f(x)= x/((e^x)-x)
Je dois donc calculer les limites et sa dérivée.
Pour la dérivée je trouve:
f'(x)=[1((e^x)-x)- x((e^x)-1)]/((e^x)-x)²
=[(e^x)-x(e^x)-2x]/((e^x)-x)²
=[x(((e^x)/x)-(e^x)-2]/((e^x)-x)²
En étudiant le signe, je trouve f(x)décroissant sur ]-oo;0[ et f(x)croissant sur [0;+oo[
Or, sur ma calculette, je vois que f(x) est croissant, puis décroissant et enfin croissant.
est ce que je me suis trompé pour la dérivée? Où sur le signe?
Et pour les limites, je trouve sur +oo: lim f(x)=0+
sur -oo: lim f(x) = 0-
Cela ma paraît bizarre... C'est juste?
Merci de votre aide ^^
Bonjour,
Oui tu t'es trompé dans la deuxième égalité : ce n'est pas [(e^x)-x(e^x)-2x] mais plutôt (e^x)-x*e^x (règle des signes).
Le domaine de définition de la fonction est R
Donc, ma dérivée est f'(x)=x[((e^x)/x)-(e^x)]/((e^x)-x)²
Donc f'(x) toujours positif
Vérification avec la calculette, Ok
Mais, si je met ma fonction f(x)=x/((e^x)-x)
elle devrait être toujours croissante or selon la calculette elle est croissant sur ]-oo;1] (environ) puis décroissant sur ]1;+oo[...
Puis, ça ne colle pas avec les limites trouvés?
Laisse donc ta calculatrice dans le tiroir, elle ne te sert à rien.
Ok pour ton domaine (en espérant que tu aies bien saisi pourquoi ...)
A présent, ce sont les limites aux bornes du domaine qu'il te faut aller chercher, et non pas la dérivée.
Le domaine de définition nous est donné ^^
Mais on aurait pu le trouver seul car x s'étend de -00 à +00 et e^x s'étend de 0 à +00 (?)
Pour les limites:
En +00:
Limite de x--> +
Limite e^x--> + car limite de x= +
car limite de x= +
Mais limite (e^x)-x= FI
Pour m'en débarraser j'ai mis x en facteur au numérateur et dénominateur:
(x*1)/x*((e^x)-1)
Les x s'annule donc --> 1/((e^x)/x)-1)
Limite (e^x)/x = +
Donc limite 1/((e^x)/x)-1)=0+
Mais le faite d'annuler les x pour enlever l'indétermination... Ce que j'ai fait me paraît vraiment tirer par les cheveux
Pardonne moi mais quel charabia !!!
Par exemple ça, c'est faux ==>Mais on aurait pu le trouver seul car x s'étend de -00 à +00 et e^x s'étend de 0 à +00 (?)
Si t'es ok on reprend tout à zéro.
Je suis complétement d'accord pour tout reprendre de zéro
et ça ne m'étonne pas vraiment que ce soit faux...
Bon.
Tu as :
Donc, il te faut un dénominateur différent de 0, tu es ok ?
Donc il te faut vérifier que
Ok!
Dans une autre questions, on a justifier que pour tout x, (e^x)-x est strictement positif.
donc, j' ai étudié ses variations (avec sa dérivée), là, j'ai montré que c'était décroissant entre ]-oo;0[
puis croissant pour [0;+oo[
En calculant x=o j'ai montrer que son minimum était 1
e
Donc, dans une question plus tôt, j'ai montré que (e^x)-x 1 donc (e^x)-x
1 donc (e^x)-x 0
0
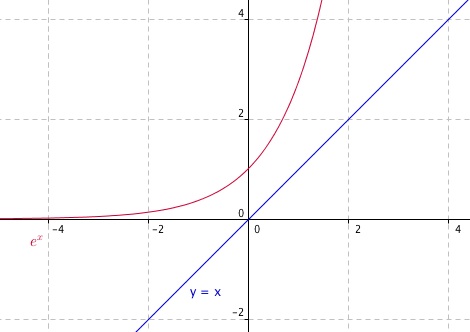
Or, d'après ton cours (voir courbe), tu sais que la courbe de l'exponentielle (en rouge) ne coupera jamais la droite y=x ci-dessous en bleu.
Donc tu auras toujours
Donc
Donc limites en -00:
lim x = -00 donc lim(e^x)=0
Lim (e^x)-x = +oo (car - devant le x)
Mais on se retrouve avec une Forme Indéterminé de la forme  /
/
Donc on met x en facteur?
Je ne comprends rien de ce que tu marques ....
lim x = -00 donc lim(e^x)=0 <== qu'est)ce que cela veut dire ?
Ok, donc pas de divison par 0.
Déjà, Limite de x= -00
Donc je dirais qu'on se retrouve avec - /+
/+
(Car lim-x=+ )
)
Donc une FI.
Mais, vous me dites que c'est pas ça, mais je vois pas autrement vue que lim (e^x)-x=+
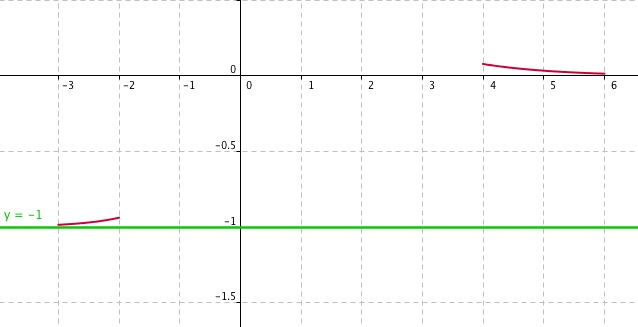
limite de f(x) en - = -1 ==> la courbe représentative de f admet une asymptote d'équation y=-1
= -1 ==> la courbe représentative de f admet une asymptote d'équation y=-1
En + : lim 1/(((e^x)/x)-1)=0+ ==> la courbe représentative de f admet une asymptote d'équation y=0, donc l'axe des abscisses
: lim 1/(((e^x)/x)-1)=0+ ==> la courbe représentative de f admet une asymptote d'équation y=0, donc l'axe des abscisses
Et grâce à la dérivée, on sait qu'elle est croissant jusqu'à, environ 0.5 puis décroissant.
(car, f'(0)=1)
Non, je me suis trompé, c'est croissante jusqu'en 1.
f'(0)=1
mais f(o)=0
Je sais pas comment justifier dans le tableaux pour montrer que f(x) est croissant après 0
Je suis un cheminement (en tout cas, j'essaye)
Vous me montrer les 2 asymptotes trouvé grâce au limite, d'accord.
Mais, il faut bien calculer la dérivée, pour savoir si c'est croissant ou non?
Oui, donc donne moi l'expression de ta dérivée plutôt que de partir pleine blinde sur des conclusion plus que hâtives.
Manifestement tu te débrouilles pas mal en maths, mais je décèle aussi des petits manques, et c'est cela que j'essaye de te faire toucher du doigt.
Si tu pars à fond, ça ne servira à rien.
D'accord, désolé.
Ma dérivées:
de la forme u/v donc (u'v-uv')/v²
f'(x)=[1(e^x-x)-x(e^x-1]/((e^x)-x)²
=[(e^x)-x-x(e^x)-x]/((e^x)-x)²
=[(e^x)-x(e^x)/((e^x)-x)²
Et je laisse comme ça, on peut savoir le signe de la dérivée plus facilement que si on mettait x en facteur.
je ne comprends pas le (1-x)e^x
On est bien dans une dérivée de la forme u/v ?
Avec u=x
Et v= e^x-x
u'=1 et v'=e^x-1 car (e^x)'=e^x
Donc