Inscription / Connexion Nouveau Sujet
limite et forme indéterminée
Bonjour, je bute sur une question d'un exercice. Je dois trouver la limite en - l'infini de la fonction f(x)=x+1+racine(x²+4x) mais je me retrouve toujours dans des situations avec une forme indéterminée... Comment faire?
Merci
J'ai suivit ce que tu as commencé, je me retrouve avec f(x)=x+1+x(1+2/x) et ensuite j'étudie la limite en - l'infini et je trouve - l'infini. Mais j'ai fais un graphique de la fonction avec Sinequanon et la limite est censée être 1 mais je ne trouve pas mon erreur.
(graphique ci-joint)
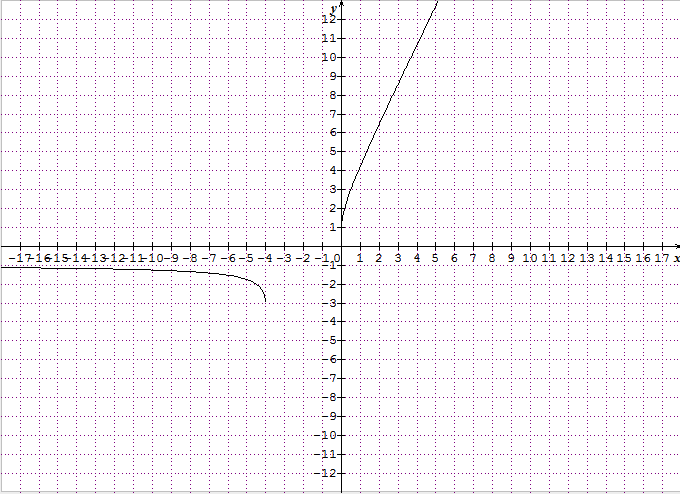
zut je viens de trouver une erreur mais sa ne change pas ma limite....
c'est f(x)=x+1+x(1+2/rac(x)) et pas f(x)=x+1+x(1+2/x)
du coup il ne fallait pas développer plus, donc je me retrouvais avec f(x)=x+1+x*rac(1+4/x)
en étudiant la limite en - l'infini de cette dernière expression, je trouve toujours moins l'infini...
Mon graphique est bon je pense donc ce n'est pas normal non?
en plus clair, j'ai:
limite lorsque x tend vers -l'infini de f(x)=x+1+x+rac(1+4/x)=-l'infini mais en comparant sur mon graphique, la limite est censée être -1. (là c'est plus clair) quelqu'un arrive-t-il à trouver -1 ou quelqu'un sait-il d-où vient mon erreur?
bonjour,
f(x)=x+1+rac(x²+4)
f(x)=x+1+rac x²[1+4/x²]
f(x)=x+1+x*rac(1+4/x²)
.........
Es tu sûre que l'on peut passer de la deuxième à la troisième étape? Ce ne serait pas plutôt uniquement avec les additions que l'on peut simplifier la racine? (même si ce n'est pas la bonne fonction ici.)
je ne trouve toujours pas.
Voici une partie de l'énoncé:
f est la fonction définie sur l'ensemble ]-oo;-4]U[0;+oo[ par: f(x)=x+1+rac(x²+4x) C est sa courbe représentative dans un repère orthonormal. 1. calculez les limites en +oo et -oo
Limite en +oo:
lim(x->+oo) f(x)=+oo
Limite en -oo:
lim(x->-oo) f(x)=?????
Je n'arrive toujours pas à me débarrasser des formes indéterminées et je reste perplexe sur la modification de la racine.(le post du dessus)



