Inscription / Connexion Nouveau Sujet
limites fonctions ln
Bonsoir 
on a la fonction prolongeable par contiuité tel que : g(x)= ( ln(x+1) )/x si x different de 0
g(0)=1
j'ai a demontrer que la lim x->0 (g(x)-1)/x = 1/2 voila ce que j'ai fait d'abord , pourriez vous me dire ou est la faute ? j'ai essaye une autre methode et ca a marché mais je ne comprends pas pourquoi celle -ci est fausse
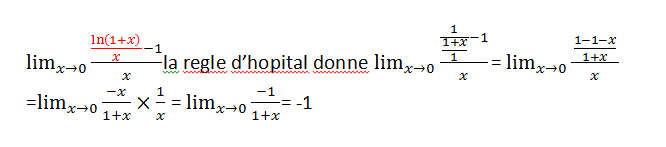
salut
il faudrait dériver correctement .... quand on applique la règle du Marquis de l'Hospital ....
don u(x)/v(x) a même limite que u'(x)/v'(x)
u(x) = .... ? donc u'(x) = ... ?
v(x) = .... ? donc v'(x) = ....?
Bonjour,
J'ai l'impression que tu te trompes dans les dérivées en appliquant la règle de l'Hôpital.
La limite de est égale à celle de :
qui est égale à la limite de
On applique encore une fois la règle de l'Hôpital, et on aboutit à étudier la limite de :
Sauf erreur.
Nicolas
salut ! mercii beaucoupppp pour vos reponses !!! concernant la regle de l'Hopital , on ne peut pas l'appliquer juste la ou on a l'indetermination comme dans ln(1+x)/x dans mon probleme ?? il faut donc l'appliquer a toute l'expression ?? si on avait
lim x->+∞ (x+2) ( 1+ln(x)/x ) peut -on appliquer cette regle juste a lnx /x ?
La réponse est dans l'énoncé même de la règle : il faut l'appliquer à l'ensemble de l'expression dont tu cherches la limite.
Annuler
connectez vous