Inscription / Connexion Nouveau Sujet
Math seconde vecteurs
*[/b][/sub]Bonjour,je ne sais pas comment trouver les coordonnées des points a partir d'un repéré,par exemple les coordonnées des points E et F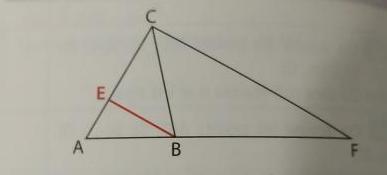
* malou > Image recadrée, sur la figure uniquement 
Un modérateur va sûrement te supprimer ta photo car il est interdit de poster son énoncé en photo. Je comprend pas trop pourquoi d'ailleurs hormis pour une économie de stockage sur leur serveur, mais bon c'est dommage parce que c'est plus pratique je trouve.
Enfin bref, prend une feuille et trace ton repère, avec tes deux vecteurs et
, tu pourras ensuite voir que pour aller de ton origine donc A jusqu'à F, il faut appliquer combien de fois
et
.
Tu pourras alors écrire : F(x,y) avec x le nombre de fois qu'on applique et y le nombre de fois qu'on applique
pour aller a F.
Bonjour,j'ai une question.J'ai un dm en maths et j'ai mal à faire un exercice.
En fait ABC est un triangle.E et F sont les points tels que le vecteur AE=1/3 vecteur AC et le vecteur AF = 3 fois vecteur AB.
Pour commencer je dois carculer les coordonnées des points E et F a partir d'un repéré (vecteur A , vecteur AB , vecteur AC)
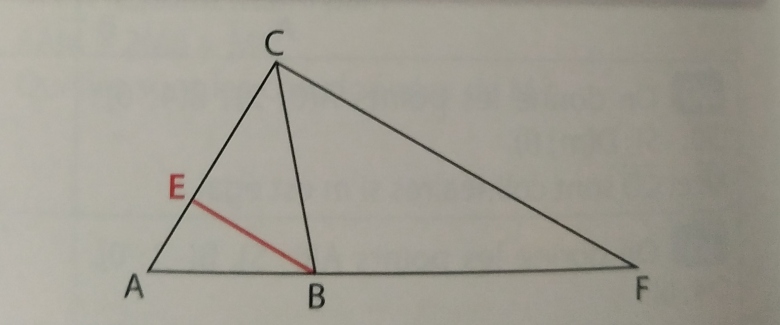
*** message déplacé ***
Bonjour,
les points E et F sont sur les axes des coordonnées de ce système
leurs coordonnées sont donc immédiates.
évidemment il faut comprendre ce que veut dire un repère (vecteur A , vecteur AB , vecteur AC)
(A est l'origine du repère, ce n'est pas un vecteur !!  )
)
c'est à dire connaitre son cours sur ce sujet des repères en général
*** message déplacé ***
E est sur l'axe des ordonnées (la droite (AC) !!) donc son abscisse est nulle
sans aucun calcul
combien vaut AE avec AC comme unité ? c'est ça l'ordonnée
et ça se lit directement dans l'énoncé
terminé pour E
on peut dire aussi que par définition dans un repère (A; vecAB, vecAC)
les coordonnées d'un point M quelconque sont les nombres x et y tels que
vecAM = x*vecAB + y*vecAC
la simple lecture de l'énoncé donne immédiatement les coordonnées demandées
(car l'énoncé définit justement vecAE !!)
c'est ça comprendre (et connaitre) son cours sur les repères...
*** message déplacé ***
Pour E c'est pas plus compliqué en réalité simplement que pour F t'as réussi car AF est supérieur à AB, donc tu as visualiser qu'il fallait 3 fois AB pour arriver a AF.
Pour AE la seule différence c'est que AE est inférieur à AC, mais tu peux quand même le ré exprimer par le vecteur AC.
Indicie : les coordonnées x ou y d'un point peuvent être inférieur a 1.
Si tu as encore besoin d'aide essaye de recopier ton énoncé parce que maintenant je n'y ait plus accès.
En fait ABC est un triangle.E et F sont les points tels que le vecAE=1/3 vecAC et le vecAF = 3 fois vecAB.
Pour commencer je dois calculer les coordonnées des points E et F a partir d'un repéré (A , vecAB , vecAC)
Pour F c'est (3;0) et pour E je suppose que c'est (0;1/3) mais je ne suis pas sur.
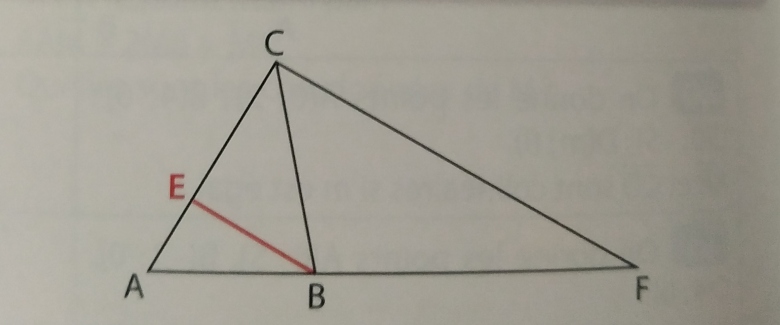
Non,ensuite je dois calculer les coordonnées de vecBE et vecCF et justifier que ils sont colinéaires.
Quand je calcule les coordonnées du vec BE je trouve (0;-2/3) et pour le vec CF(2;0)
Non c'est pas les bons vecteurs.
Tu as vu dans ton cours comment on définit un vecteur à partir des coordonnées de 2 points?
Normalement oui, sinon :
** image supprimée **
Bonjour,j'ai un problème pour résoudre un exercice sur les vecteurs.
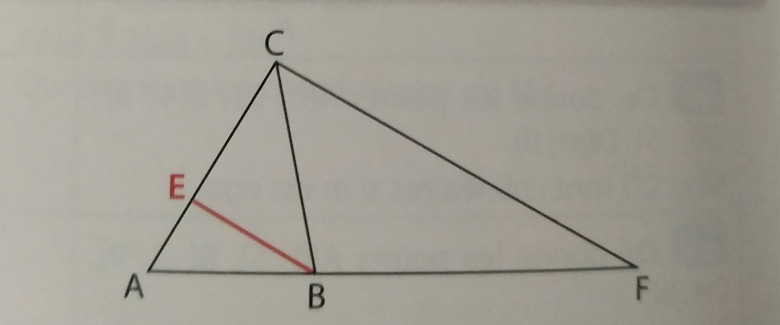
ABC est un triangle.E et F sont les points tels que vecAE=1/3vecAC et vecAF=3fois vecAB.(je laisse une photo avec la figure)
Il faut calculer les coordonnées de A,B,C,E,F a partir d'un repère (A,vecAB,vecAC).
J'ai trouvé pour A(0;0),B(1;0),C(0;1),E(0;1/3)F(3;0)
Ensuite il faut calculer les coordonnées des vecteurs: vecBE et vecCF.
Moi j'ai fait pour le vecBE=0-1=-1; 1/3-0=1/3.
Donc j'ai trouvé vecBE a pour coordonnées (-1;1/3);
Pour le vecCF=3-0=3; 0-1=-1.
Donc le vecCF a pour coordonnées(3;-1)
Ensuite il faut justifier que le vecBE et le vecCF sont colinéaires et faire la conclusion.
Le problème c'est que deux vecteurs sont colinéaires si l'un est un multiple de l'autre mais dans mon cas c'est pas comme ça.
Je ne sais pas où j'ai faux.
Merci d'avance.
*** message déplacé ***


 guide latex
guide latex présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le  mode d'emploi du forum
mode d'emploi du forum


