Inscription / Connexion Nouveau Sujet
Maths sur parallépipède rectangle
Bonjour
Je suis en seconde, j'ai un devoir maison à rendre et je suis bloqué a la question 1.
si vous pouvait me donner un coup de main sa serait bien, merci😊
ENONCE:
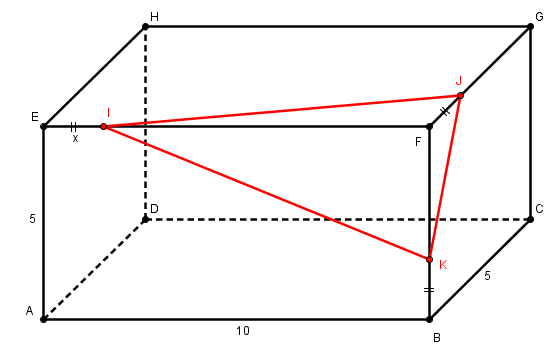
On considère le parallélépipède rectangle ABCDEFGH avec AB=10cm et BC=BF=5cm.
On place les points I,J et K sur les segments [EF], [FG] et [BF] tels que EI=FJ=BK=x On appelle pavé tronqué le solide obtenu en enlevant le tétraèdre FIJK au pavé.
QUESTION:
1)Est-il possible de placer I de telle sorte que le volume du 《pavé tronqué》soit égal à 245cm cube?
Je ne sais pas trop par ou commencer et par ou traiter la question, n'y quoi faire.
merci de m'aider☺
Il s'agit de calculer, en fonction de x , le volume du pavé tronqué.
Ce pavé tronqué résulte du retrait du tétraèdre hors du parallélépipède. Les dimensions de ce dernier, donc son volume, sont connus.
Reste à à calculer le volume du tétraèdre.
Déjà, merci de m'avoir répondu et si j'ai bien compris il faut faire parrallélépipè rectangle-le tétraèdre donc je fais:
Volume parrallélépipède rectangle= c×c×h=10×5×5
=50×5
=250cm cube
jusque ici ça va mais après je n'est pas compris a part ça:
Volume tétraèdre=B×h/2
Bonjour,
ne pas confondre hauteur du triangle FJK dont la base (du triangle) est bien choisie FJ et la hauteur correspondante (du triangle) = FK
et hauteur du tétraèdre associée à la base FJK qui est bien FI
donc dans la formule du volume on a bien
base (= aire du triangle ) = FJ×FK/2= x×(5-x)/2
et hauteur (du tétraèdre) = FI = (10-x)
une figure jointe aurait évité de se mélanger les pinceaux :
y a plus qu'à remplacer...
désolé mais je n'arrive pas à voir une valeur précise de x car j'ai:
x(5-x)/2×(10-x)/3 mais après je ne sais pas faire
Je peux peut être développée mais je crois ça ne marche pas ce que j'ai fait:
5x-xau carré/2×(10-x)/3
=15x-x aucarrée -x/2/3
=14x-x au carré /2/3
donc je fais quoi?
le volume du tétraèdre est donc bien
VT = x(5-x)/2×(10-x)/3 = x(5-x)(10-x)/6
et puis ça peut tout aussi bien rester comme ça pour l'instant
en tout cas si on le développe au moins il ne faut pas faire des erreurs
si on développe (correctement) on obtient un terme en x3 (x au cube !!) incontournable et qui ne disparaitra jamais du problème
conséquence : en seconde on ne pourra aboutir au final que de façon approchée à la calculette.
(tableau de valeurs, ou lecture graphique)
en tout cas la suite est de calculer le volume du pavé tronqué
V(x) = V pavé - VT = 250 - x(5-x)(10-x)/6
et d'écrire ce que l'on cherche à résoudre (de traduire l'énoncé) :
on veut V(x) = 245
donc 250 - x(5-x)(10-x)/6 = 245
ou encore
x(5-x)(10-x)/6 = 5
qui est l'équation à résoudre
et comme j'ai dit, ça ne peut se faire que à la calculette ...


