Inscription / Connexion Nouveau Sujet
Mesure principale d'angle
Bonsoir, nous venons de commencer un nouveau chapitre mais j'ai du mal à comprendre /:
Déterminer dans chaque cas la mesure principale de l'angle dont une mesure est donnée
a) 5 /4 b) -4
/4 b) -4 /3 c) -10
/3 c) -10 /3
/3
d) 135 e) 185
e) 185 /6 e) 17
/6 e) 17 /13
/13
Avez-vous une métholde ? Une définition pour mieu comprendre et réalisé ce type d'exercice ?
Bonne soirée !
Il existe des méthodes pour déterminer la mesure principale d'un angle.
En voici une : ![]() .
.
Mais il est parfois plus simple de la calculer en déterminant la position du point sur le cercle trigonométrique représentant l'angle.
Tu as déjà fait cet exercice il y a quelques jours...
Te souviens-tu de cette figure ?
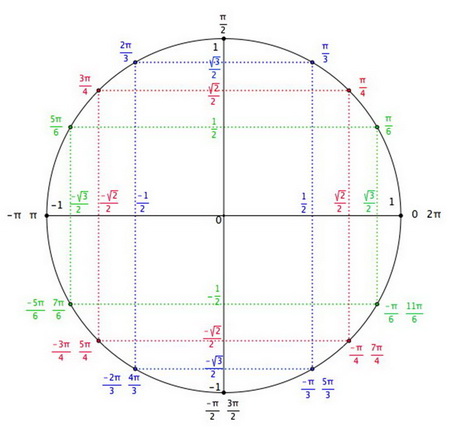
Merci de ta réponse. Oulala c'est un peut dur :/ que veux-tu dire par "Mais il est parfois plus simple de la calculer en déterminant la position du point sur le cercle trigonométrique représentant l'angle" ?
Je prends par exemple l'angle .
Cet angle n'appartient pas à puisque
.
Retirons-lui l'équivalent d'un tour complet, soit .
.
Or .
La détermination principale de est
.
Tu vois que la méthode est simple... (et cela se confirme sur le dessin que tu as sous les yeux)
Il faut ajouter ou soustraire un ou plusieurs tours complets pour que la détermination principale soit dans l'intervalle
Merci pour cette exemple! Parcontre ma questions est : faut-il toujours ajouter 2Pi ou soustraire 2Pi ? Pourquoi ? Quand savoir quand il faut soustraire ou ajouter ? Pouvez-vous me donner un autre exemple pour que je puisse le faire ?
Merci !
faut-il toujours ajouter 2Pi ou soustraire 2Pi ? Pourquoi ?
Ajouter ou soustraire
La seule chose qui change, c'est la valeur de la mesure de l'angle.
Comme je viens de l'écrire : Il faut ajouter ou soustraire un ou plusieurs tours complets pour que la détermination principale soit dans l'intervalle
Il faut soustraire quand l'angle est supérieur à
Je prends l'exercice b) : l'angle
Cet angle n'appartient pas à
Ajoutons-lui l'équivalent d'un tour complet, soit
Or
La détermination principale de
Oui, si tu parles de la lettre d'hier, c'est bien ce que tu dis...
Regarde le dessin que je viens de t'envoyer à 21h00.
Les deux angles sont bien représentés par le même point.
je vais essayer de faire le C : -10 /3+2
/3+2 *3/
*3/ = -10
= -10 /3+6
/3+6 /3 mais ensuite la je ne sais pas si je dois continuer à ajouter un tour ou pas ?
/3 mais ensuite la je ne sais pas si je dois continuer à ajouter un tour ou pas ?
Ah, en gros tant que je vois que mon résultat n'est pas compris en Pi et -Pi je continue mon ajout/soustraction de tours ?
C'est un bon début, mais la réponse finale n'est pas dans l'intervalle
C'est d'ailleurs l'exemple que j'ai donné à 21h47.
Tu a ajouté , mais il fallait ajouter
Oui j'ai vue c'est la même chose, mais étant donner que je suis partie de -10Pi/3 pour moi c'est extraordinaire 
Oups...
Je remarque que j'ai loupé un crochet ! (tellement l'habitude de les fermer...)
Il s'agit de l'intervalle (crochet ouvert à gauche...)
Pourquoi fait-on 134Pi+ Pi ?
et pourquoi n'enlevons pas de tours ? C'est cela que je n'arrive pas à comprendre
Comme tu le dis, on peut enlever des tours complets.
Ecrire ceci : revient à écrire ceci :
La détermination principale de est




