Bonjour je bloque sur cet exercice, pouvez-vous m'aider ?

x désigne un réel tel que :

0 < x < /2

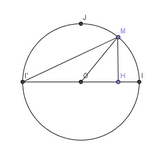
Sur le cercle trigonométrique C représente ci-conte, M est le point associé au réel X.

H est le point de la droite (OI) tel que le triangle OHM soit rectangle en H.

1. (a) Justifier les égalités suivantes :

- I'H = 1 + cos x
-cos ( x/2 ) = I'H / I'M
-cos ( x/2 ) = I'M / 2

   (b) En déduire  que cos² (x/2) = 1 + cos x / 2