Inscription / Connexion Nouveau Sujet
Mise en équation
Bjr,
Enoncé:
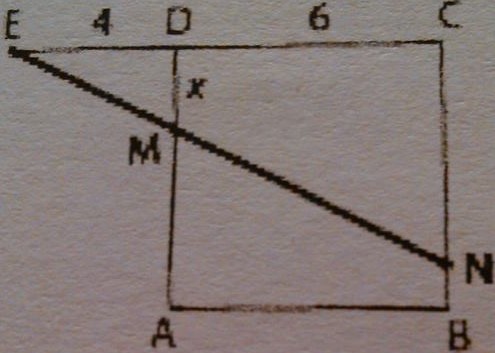
ABCD est un carré de côté 6cm et DE= 4cm. M est un point du segment [AD]. La droite (EM) coupe le segment [BC] en N. On se propose de trouver M tel que DM=BN.
On pose DM= x
1- Démontrez que x [0;12/5].
[0;12/5].
2-a) Calculez CN en fonction de x.
-b) Déduisez-en BN.
3- Existe-t-il une valeur de x pour laquelle DM= BN ?
Je pense qu'il faudra utiliser Thales pour la question 2- sinon pour les autres je ne vois pas comment faire.
x ne peut pas être inférieur à 0 car c'est une distance, et il ne peut pas être plus grand que la distance DM
Observe les positions extrêmes du point N. A l'une d'elles correspond la position du point M pour laquelle x est maximal. C'est cette dernière valeur de x que tu peux calculer par Thalès.
Pour la question 2-a):Avec Thales j'obtiens: 10 x/4 = 2.5x.
x/4 = 2.5x.
Mais cela ne peut pas être possible car un coté fait 6cm,et visuellement CN parait faire bcp plus de la moitié du coté
Non c'est correct.
La distance CN n'est pas fixe comme sur la figure, elle dépend en fonction de x !
Le point N peut se déplacer sur le côté du carré. De quel point à quel point ?
Le point M se déplace en même temps. Pour quelle position de N la longueur MD = x sera-t-elle maximale ?
On sait que :
DM = x
BN = 6-2,5x
On te demande s'il existe une situation où DM = BN
Quelle équation faut-il résoudre alors ?
Si elle a des solutions, oui il y a une situation où DM = BN
Sinon il n'y en a pas
Oui enfin on veut la valeur exacte ! qui est 12/7 !
Comme cette solution est comprise dans l'ensemble de définition (trouvé à la question 1) elle est valable donc il y a bien une situation où DM = BN


 1.71
1.71
