- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
moyenne loi normale vs distribution log-normale
Bonjour,
Je suis un peu confus par un problème sur la distribution log-normale :
F est la vraie moyenne de la fluorescence d'une population de bactéries.
On cherche à mesurer ce paramètre avec Yi = Xi*Ei
Avec Xi la valeur du paramètre et Ei une erreur de mesure
Les Ei sont log-normaux avec moyenne 0 et écart-type 0.1
Les Xi sont d'abord supposés avoir une valeur identique X. Dans un 2ème temps, on dira que les bactéries émettent individuellement différents niveaux de fluorescence et la distribution sera log-normale de paramètres inconnus mu and sigma.
On définit le changement de fluorescence comme :
C= log(X/F) dans le cas des Xi identiques
C = log(e^mu / F) dans le cas des Xi log-normaux.
L'estimateur empirique du changement est donc C_hat= log(Yi/F)/n.
Quelle distribution suivent log(Yi/F) et C_hat dans chaque cas et quel test utiliser pour tester l'hypothèse que C_hat = C, avec C_hat = 0.01 (et un écart-type de 0.2 pour le second cas) ?
Ce que j'ai dit est que pour des Xi identiques, log(Yi/F) = log(Ei*Xi/F). log(Xi) - log(F) = 0, donc on se retrouve avec log(Ei) seulement.
Donc log(Yi/F) suit une distribution normale (0,0.1) comme log(Ei).
C_hat est aussi normal avec la même moyenne et un écart-type = sigma/sqrt(n)
On utilise un test avec la statistique Z=(C_hat-C)/(sqrt(sigma)/n)
Mais dans l'autre cas je ne sais pas dire quelle loi suivent log(Yi/F) et C_hat et quel test utiliser.
On a à nouveau :
log(Yi/F) = log(Ei) + log(Xi) -log(F).
The log(Xi) and log(Ei) sont normaux donc les paramètres seraient la somme des moyenne et la somme des écart-types.
Mais il reste log(F).
D'après la définition C = log(e^mu / F) j'aurais tendance à dire que log(e^mu) = log(F).
Les log(Xi) seraient donc centrés sur 0.
Mais sur wikipédia (voir image jointe) il semble que la moyenne mu d'une distribution log-normale (moyenne de la distribution normale obtenue en prenant le log) n'est pas égal au log de la moyenne m de la distribution originelle.
C'est-à-dire que log(e^mu) est différent de log(F).
C'est ici que je bloque, donc je ne suis pas sur de la distribution et des paramètres pour log(Yi/F) et C_hat, et quel test d'hypothèse il faudrait appliquer ensuite pour mesurer un changement entre C et C_hat
Merci beaucoup pour votre aide !
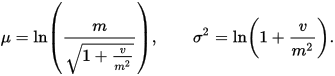


 statistiques en post-bac
statistiques en post-bac