Niveau terminale

Nombre complexes et géométrie

Posté par
Holin 03-09-11 à 14:42

Bonjour alors cela fait déjà 3 jours que je recherche sans relache une solution à cet exercice :

Le plan complexe est muni d'un repére orthonormal (O, u, v) d'unité 3 cm
Soit A et B les points d'affixes respectives za = 2 et zb = √2 +i√2
Le point I d'affixe zi est le milieu du segment [AB]

1) Donner le forme trigonométrique de zb :

module de zB = √ ( √2 )² + (√2 )² ) = 2
cos = √2 /2
sin = √2 /2
Donc arg(zB) = pi/4

zb = 2(cos pi/4 + i sin pi/4)

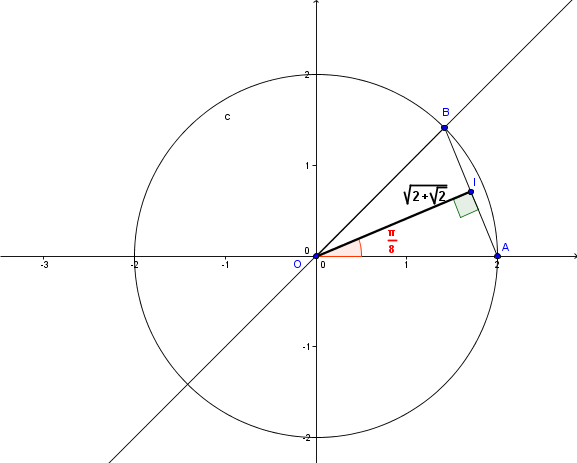
2) Placer avec précision les points  A, B, et I dans le repère;On expliquera le raisonnement concernat le placement des points B et I
Sa je sait le faire

3) a) Donner la forme algébrique de zI puis déterminer le module de zI

zI = (za +zb) / 2 = (2 + √2  + i√2 ) / 2 = (2+√2 )/2 + i*√2 /2

module de zI = √ [ ( (2+√2 )/2 ) ² +( √2 /2 ) ²] = ???? il y a des racines de racines et je ne sais pas comment faire

b) Déterminer Arg(zI)

La je séche je trouve toujours des resultats différent en fonction des module de I que je trouve mais qui sont faux

c) Donner la forme trigonométrique de zI

Je peut evidemment pas faire sans arg de I

4) En déduire les valeur exactes de cos(pi/8) et  sin (pi/8)
Je ne peut en déduire car j'ai pas fait entièrement le 3

5) Déterminer les valeurs exactes de cos (3pi/8) et de sin (3pi/8)
iDEM

Merci d'avance pour tous ceux qui m'aiderons dans la résolutions de ce problème

Posté par re : Nombre complexes et géométrie 03-09-11 à 15:13

Bonjour,

Un dessin ?

Nombre complexes et géométrie

Posté par re : Nombre complexes et géométrie 03-09-11 à 16:08

Bonjour Holin, bonjour Cailloux

il ne faut pas se laisser impressionner par ces racines de racines, je pense que tu étais sur la bonne voie et le schéma de Cailloux doit t'aider et te conforter ds tes recherches.

Ce schéma met en évidence que $\rm Arg(z_i)=\frac{\pi}{8}$ .

reste à le démontrer :

Tu as dû trouver que $\large\rm z_i=\frac{2+\sqrt{2}}{2}+i.\frac{\sqrt{2}}{2}$ , dc que le module de $z_i$ est $\rm\sqrt{2+\sqrt{2}}$ .

on en déduit que (Cf le cours), en désignant par $\rm\alpha$ l'argument de $\rm z_i$ :

$\large\rm \cos\alpha=\frac{x}{\sqrt{x^2+y^2}} ; \sin\alpha=\frac{y}{\sqrt{x^2+y^2}}$

avec : $\large\rm x=\frac{2+\sqrt{2}}{2} ; y=\frac{\sqrt{2}}{2}$

Après développements et simplifications, tu dois trouver que :

$\large\rm\cos\alpha=\frac{\sqrt{2+\sqrt{2}}}{2}  ;  \sin\alpha=\frac{1}{\sqrt{2}.\sqrt{2+\sqrt{2}}}$

Le produit $\cos\alpha\times\sin\alpha$ se simplifie en : $\frac{1}{2.\sqrt{2}}$ .

Dc $\large\rm 2.\sin\alpha.\cos\alpha=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}=\sin 2.\alpha$ .

Quels sont les angles dt le sinus vaut (à 2k près ; k) $\rm\frac{\sqrt{2}}{2}$ ?

Ce sont les angles de mesures $\rm\frac{\pi}{4}  et  \frac{3.\pi}{4}$ .

Comme le point I est situé ds le 1er quadrant (Cf graphique), la mesure cherchée est dc la moitié de $\rm\frac{\pi}{4},  soit  \frac{\pi}{8}$ .

D'accord ?

Posté par re : Nombre complexes et géométrie 03-09-11 à 16:23

L'écriture trigonométrique de $\rm z_i$ est dc : $\large\rm\sqrt{2+\sqrt{2}}.\left(\cos\frac{\pi}{8}+i.\sin\frac{\pi}{8}\right)=\frac{2+\sqrt{2}}{2}+i.\frac{\sqrt{2}}{2}$ .

De cette écriture, on déduit que :

$\large\rm\cos\frac{\pi}{8}=\frac{2+\sqrt{2}}{2.\sqrt{2+\sqrt{2}}}=\frac{\sqrt{2+\sqrt{2}}}{2}$

et

$\large\rm\sin\frac{\pi}{8}=\frac{\sqrt{2}}{2.\sqrt{2+\sqrt{2}}}=\frac{1}{\sqrt{2}.\sqrt{2+\sqrt{2}}}$

D'accord ?

Posté par re : Nombre complexes et géométrie 03-09-11 à 16:31

A noter qu'à la Q4, on retrouve les valeurs exactes qui ont servi à déterminer l'argument de z_i, et que l'énoncédonnait une indication sur la valeur à trouver.

Q5 : il suffit d'appliquer les formules trigonométriques des angles complémentaires :

$\cos\left(\frac{3\pi}{8}\right)=\cos\left(\frac{4\pi}{8}-\frac{\pi}{8}\right)=\cos\left(\frac{\pi}{2}-\frac{\pi}{8}\right)=\sin\left(\frac{\pi}{8}\right)$

ET

$\sin\left(\frac{3\pi}{8}\right)=\sin\left(\frac{4\pi}{8}-\frac{\pi}{8}\right)=\sin\left(\frac{\pi}{2}-\frac{\pi}{8}\right)=\cos\left(\frac{\pi}{8}\right)$

A ta disposition si tu as des questions

Posté par re : Nombre complexes et géométrie 03-09-11 à 17:09

Bonjour pppa,

Je pense que la géométrie suffit pour prouver que $Arg(z_I)=\frac{\pi}{8}\;\;[2\pi]$ :

On sait que $OA=OB=2$ donc que le triangle $OAB$ est isocèle en $O$ .

Sa médiane $[OI]$ est donc bissectrice de l' angle $\widehat{O}$

On a donc $(\vec{OA},\vec{OB})=2(\vec{OA},\vec{OI})=\frac{\pi}{4}\;\;[2\pi]$

et $Arg(z_I)=(\vec{OA},\vec{OI})=\frac{\pi}{8}\;\;[\pi]$

et comme les parties réelle et imaginaire de $z_I$ sont positives, on a:

$Arg(z_I)=\frac{\pi}{8}\;\;[2\pi]$

Posté par Merci 03-09-11 à 17:17

Ah ok j'i compris effectivement j'avais trouvé cela pour le module de zi mais je me suis dit que je ne pouvais pas trouvé l'argument comme ca et en fait non. Merci à tous j'ai tout compris!

Posté par re : Nombre complexes et géométrie 03-09-11 à 17:43

>> Cailloux

je pense que tu as raison, ta méthode est plus simple et + rapide, d'autant qu'on a fait calculer l'argument de z_b au préalable.

En reprenant l'énoncé de façon synthétique, je m'aperçois qu'on est bien guidé étape par étape.

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

Nombres complexes en terminale
9 fiches de mathématiques sur "nombres complexes" en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Nombre complexes et géométrie

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths