Inscription / Connexion Nouveau Sujet
Nombres complexes !
Bonjour à tous ! voilà j'ai un exercice sur les nombres complexes et j'ai du mal à faire une question
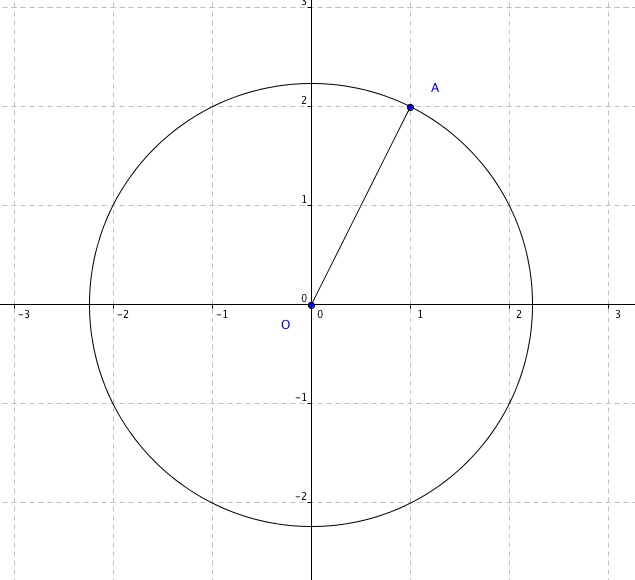
Za = 1 + 2i
Zb = Conjugué de Za
Zc = 1 +  3 + i
3 + i
Zd = Conjugué de Zc
On m'a demandé de calculer Zb-Zc/Za-Zc
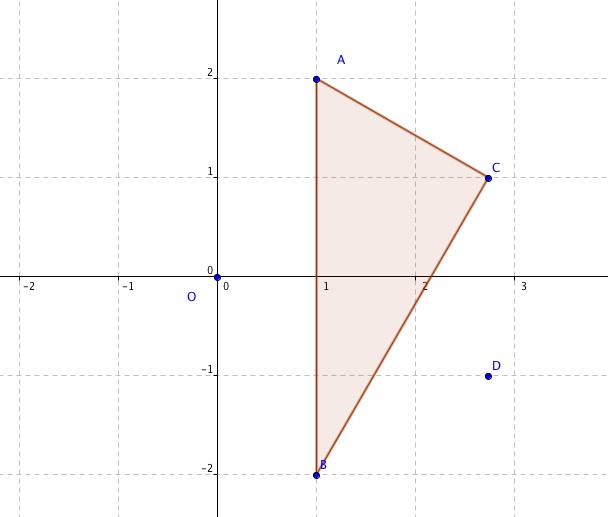
Et d'en déduire la nature du triangle
j'ai donc dis qu'il était rectangle.
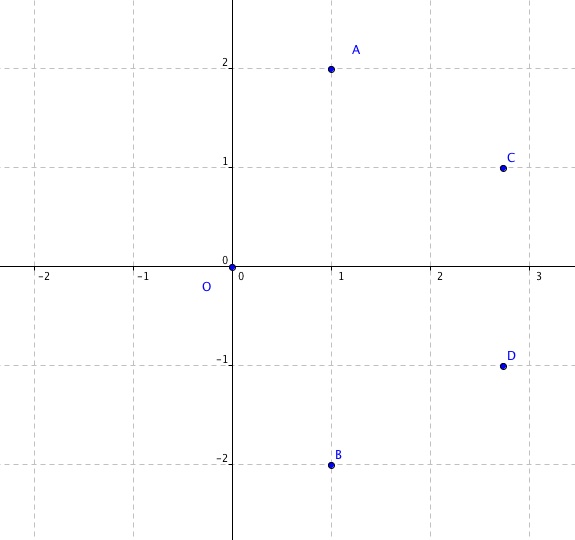
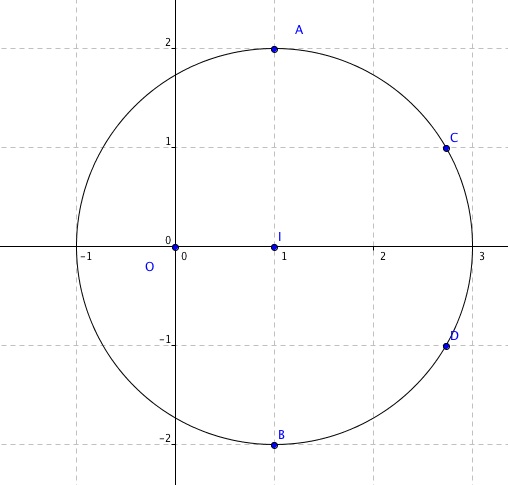
Puis on me demande de démontrer que les points A, B , C et D appartiennent à un même cercle T dont on précisera le centre et le rayon.
Je bloque ici, est-ce que vous pouvez m'aider s'il vous plait ?
C'est pas tellement cela, même si c'est vrai.
On te demande de prouver que les points sont sur un même cercle, leurs modules seront donc tous égaux.
Attend, je me demande si je ne t'ai pas dit une bêtise.
C, c'est bien
Parce que ce n'est pas ce que j'avais vu au début 
Si c'est bien cela, je t'ai dit une bêtise.
Par l'argument:
( Vecteur CA ; Vecteur CB )= Arg ( Zb-Zc/Za-Zc) = arg i 3 = Pi/2
3 = Pi/2
Donc triangle rectangle
L'idée, c'est de partir ainsi :
soit I:(x,y) le centre du cercle recherché.
J'ai
et
Tu vas ainsi obtenir 2 équations en x et y (donc à 2 inconnues), et tu en tires x et y coordonnées du point I.
Le reste ensuite pour le rayon du cercle coule de source.