Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Nombres complexesTopics traitant de nombres complexes [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Nombres complexes et géométrie

Posté par
lollipop-ins 03-01-10 à 14:01

Bonjour à tous

Je bloque sur le deuxième exercice de mon dm, qui porte sur les nombres complexes (qui n'ont jamais été ma tasse de thé )
Voici l'énoncé:

On désigne par Mn le point du plan complexe d'affixe Zn définie par:

Zn= (1/2)^n e(in*Pi/3) = (1/2)^n (cosn (Pi/3) + isin n (Pi/3))

où n est un nombre entier naturel et où Mo est le point d'affixe zo= 1

1) Déterminer les valeurs de n pour lesquelles zn est un réel
2) Le plan complexe P est rapporté à un repére orthonormal. (O; vecteur u ; vecteur v ) (unité = 8cm )
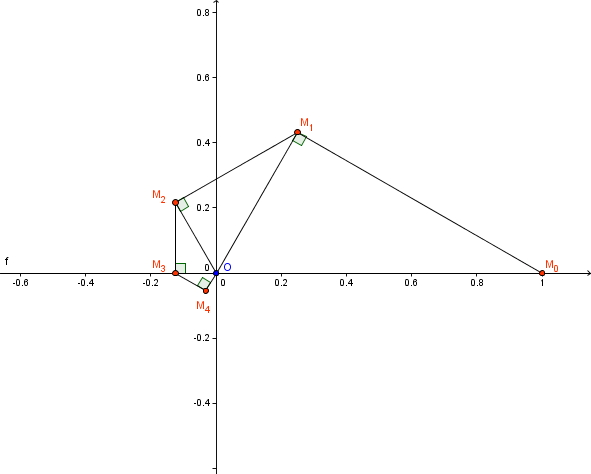
a) Représenter dans P les points Mo, M1, M2, M3, M4
b) Calculer en fonction de n les longueurs des trois cotés du triangle OMnMn+1.
Montrer que ce triangle est rectangle.

Désolée pour les notations
J'ai vraiment besoin d'aide, je bloque des la première question!

Merci d'avance.

Posté par
cailloux Correcteurre : Nombres complexes et géométrie 03-01-10 à 20:30

Bonjour,

1) Arg(z_n)=\frac{n\pi}{3}\;\;[2\pi]

Avec n\in\mathbb{N}:

z_n\in\mathbb{R}\Longleftrightarrow \frac{n\pi}{3}=k\pi\;\;\;\;k\in\mathbb{N}

Soit n=3k

2)a) un dessin:

Nombres complexes et géométrie

2)b) OM_n=|z_n|=\frac{1}{2^n}

OM_{n+1}=|z_{n+1}|=\frac{1}{2^{n+1}}

M_nM_{n+1}=|z_{n+1}-z_n|=\left|\frac{1}{2^{n+1}}e^{i\frac{(n+1)\pi}{3}}-\frac{1}{2^n}e^{i\frac{n\pi}{3}}\right|

M_nM_{n+1}=\left|\frac{1}{2^n}\left(\frac{1}{2}e^{i\frac{\pi}{3}}-1\right)\right|=\frac{1}{2^n}\left|\frac{1}{2}e^{i\frac{\pi}{3}}-1\right|

M_nM_{n+1}=\frac{1}{2^n}\left|-\frac{3}{4}+i\frac{\sqrt{3}}4{}\right|

M_nM_{n+1}=\frac{\sqrt{3}}{2^{n+1}}

et on a bien OM_{n+1}^2+M_nM_{n+1}^2=OM_n^2

ce qui prouve que OM_nM_{n+1} est rectangle en M_{n+1}


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !